WIISの述語論理の章が終わり集合論へ突入するのでその前に自分なりに論理と集合を結びつけてみます。
部分集合と含意
集合と含意は人の認識を厳密に考える為のもので、同じものであるというのが長濱説です。
含意と部分集合でそれを説明してみます。
A⊆B
AはBの部分集合であるという意味。
部分集合はどんな認識なのか。
図にするとこんな感じかと。
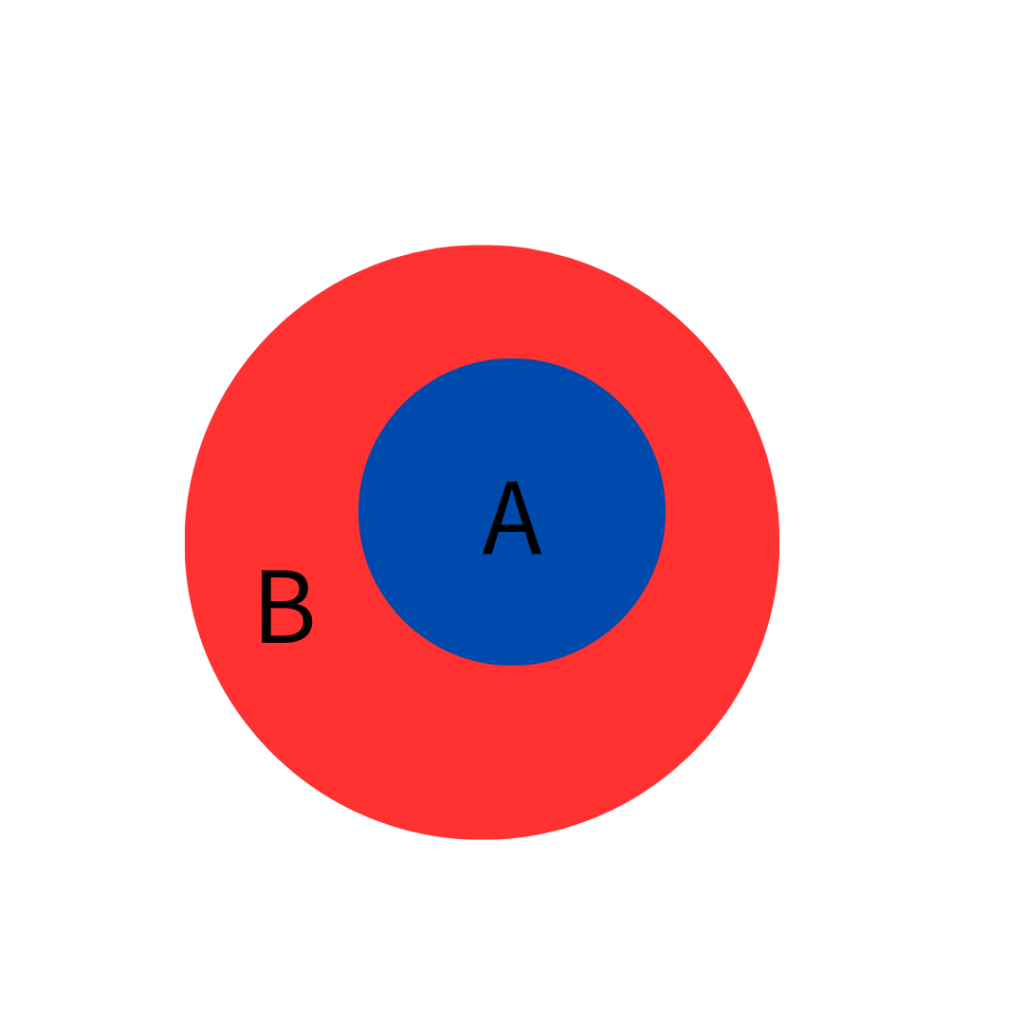
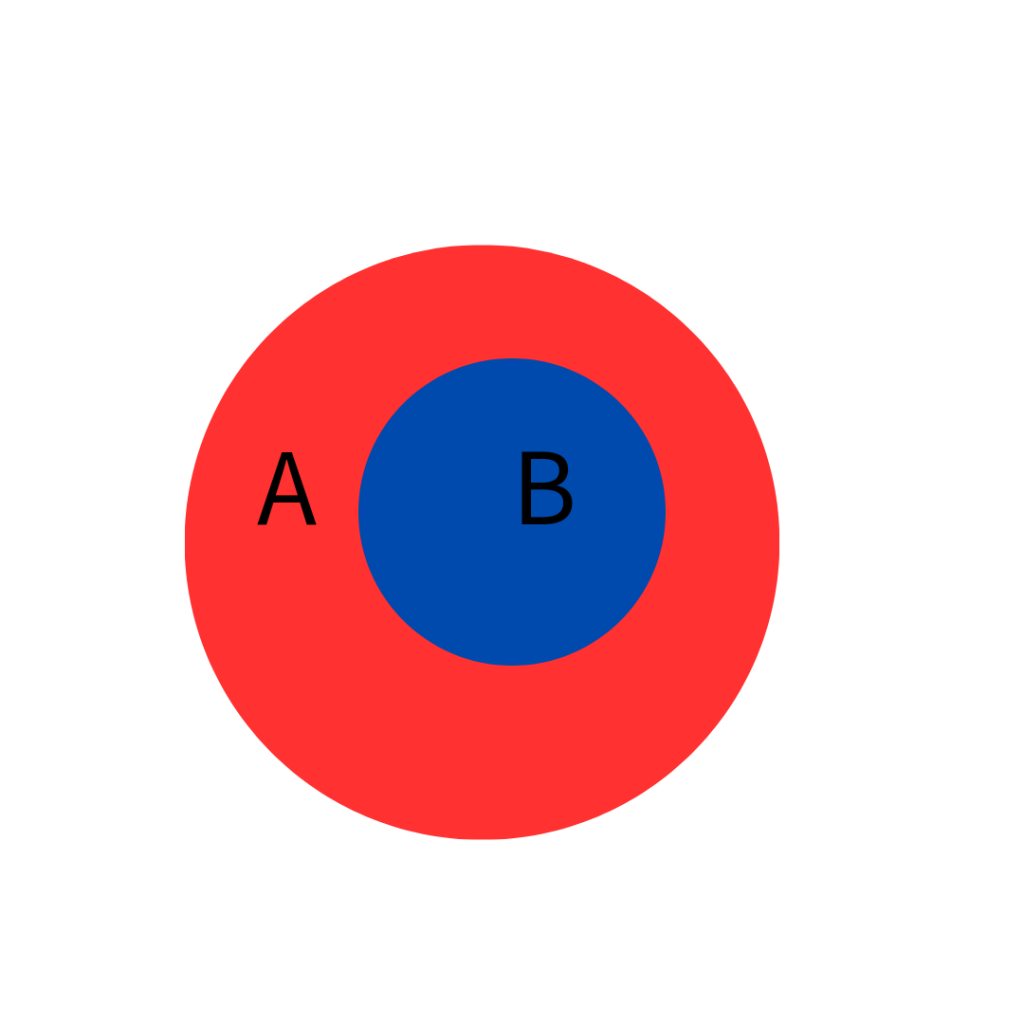

Aに含まれるならBにも含まれる。
A→B
AはBの部分集合である。
A⊆B
「Aに含まれるならBにも含まれる(AであるならBでもある)」であると翻訳できます。
人類が生活している巨視的な現実は原因と結果(順序関係)で説明されます。
A(原因)→B(結果)
Aのドミノが倒れたら必然的にBのドミノも倒れる因果関係の認識。AとBの間にある規則(関係)を考えられるのが人類です。そして、それ以外の認識は知りません。
数学や哲学の目的は人の認識とその二項関係から導き出される法則を明らかにすることかと。
認識の外側を考えようとするのが哲学の一分野である形而上学なのかなあと。認識の外側を考える方法があるとは思えないし、認識の枠組みの中でその結論を見いだす作業を行おうとすること自体が矛盾している気がしますが、面白そうな試みに感じます。
形而上学(けいじじょうがく、英: metaphysics)は、感覚ないし経験を超え出でた世界を真実在とし、その世界の普遍的な原理について理性(延いてはロゴス)的な思惟で認識しようとする学問ないし哲学の一分野[1][注釈 1][注釈 2]。世界の根本的な成り立ちの理由(世界の根因)や、物や人間の存在の理由や意味など、感覚を超越したものについて考える[2]。
Wikipedia
認識と集合論
(A→B)∧(B→A)⇔A=B⇔(A⊆B)∧(B⊆A)
同じ関係を説明していると解釈しました。
現時点での僕の捉え方です。人の認識から集合論までが隙間なく物語として繋がることが重要なので、一先ずはこの理解で進めます。


コメント