集合と概念と概念を創る | 長濱陸のブログ

以下の記事で存在についての僕の個人的なイメージが少しだけ作られました。
存在を定義する、概念を創るとは対象となる概念とそれ以外の概念との関係を明らかにすることであると現時点では納得できます。
「動物」って概念の上に何らかの関係を定義することで「犬」って概念が創られて、「動物」に内包された「犬」との関係によって「猫」って並立する概念が定義されます。
さらに「犬」の上に「ブルドッグ」「ドーベルマン」といった上位概念が関係を定義することで創られていく。

動物→犬→ブルドッグと言う風に、上へ向かうに従い情報が付加されていく構造になっているので、最下位の概念は「無」で、最上位の概念は「無限」になりますね。
これが正しいと仮定するなら、無と無限の関係を明らかにしてくのが数学だと見ることもできるでしょう。自分なりの意味付けでさらにワクワクしてきました。

「我思う、故に我在り」についてさらっと考えてみます。
デカルトは実存として確かにそこにあったのかもしれません。
が、「デカルト」という概念を定義する為の関係は上記の言葉では明らかにできていません。
つまり、数学的宇宙においては「我思う」では「我」は定義できません。
※長濱説

集合（概念）を創る

集合（概念）を創る

「集合 = モノの集まり」と考えると無秩序で捉えどころがないので、まるで奇人変人の狂った遊びって感じがしますが、「集合＝概念」と捉えると何となく以下の議論は何がしたいのかってことが受け入れやすくなります。

部分集合

部分集合は例えば、自然数の元から2で割り切れる元を全て集めた集合を新たに作り、「偶数」という概念を創りだすようなことです。
その対となる奇数も必然的に出現し、それは後述する「偶数の『補集合』としての奇数」を存在させることです。

自然数の中にある全ての元を抜き出して創った新たな集合も広義の部分集合と定義することができます。

【部分集合】
集合 A の要素はすべて集合 B の要素でもあるとき、すなわち、
$\displaystyle \forall x(x\in A\rightarrow x\in B)$
が成り立つとき、A は B の部分集合であるといい、
$\displaystyle A\subseteq B$
で表す^[1]。

A が B の部分集合であることを、「A は B に（部分集合として）含まれる（contained; 包含される）」、「A は B に包まれる（included; 包摂あるいは内包される）」などということもある。
またこのとき、B は A の上位集合（じょういしゅうごう、superset; スーパーセット）であるということもある。
B 以外の集合で B の部分集合であるようなものは、B の真部分集合（しんぶぶんしゅうごう、proper subset）あるいは狭義（strict; 強い意味で）の部分集合と呼ばれる。
すなわち、集合 A が集合 B の真部分集合であるとは、A ⊆ B かつ A ≠ B が成り立つことである。A が B の真部分集合であることを

$\displaystyle A\subset B$
で表す。
Wikipedia

集合Aの任意の元が全て集合Bに含まれることを「AはBの部分集合である」と呼び、Aの全てがBに含まれていて、かつAがB自体でない場合を「真部分集合」と呼びます。
定義上「A＝A」も部分集合に含まれるため、混乱を避けて議論を行いたい場合用に狭義の部分集合が定義されているのでしょう。

ところで、冒頭では「動物」は「犬」の下位概念と表現しましたが、集合では上位概念（集合）と定義されていますので、混乱を避けるために今後「上位概念」という言葉を使う時は、集合の定義に合わせて使用します。つまり、「動物」の上位は「犬」「0」が最下位概念で「無限」が最上位概念。

差集合

集合 B から集合 A に属する元を間引いて得られる集合を
$\displaystyle B\setminus A,\quad B\smallsetminus A$

または B − A と表現し、B から A を引いた差、差集合あるいは B における A の（相対）補集合と呼ぶ。記号を用いて書けば、
$\displaystyle x\in B\setminus A\iff x\in B\land x\notin A,$

すなわち
$\displaystyle {\begin{aligned}B\setminus A&=\{x\mid x\in B\land x\notin

A\}\\&=\{x\in B\mid x\notin A\}\end{aligned}}$

が差集合の定義である。
Wikipedia

シンプルな定義ででWikipedia画像がイメージしやすい。

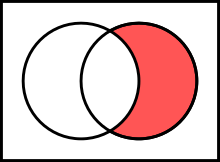
右 – 左のイメージ。
赤が差集合。

右 – 左のイメージ。
赤が差集合。

補集合

全体集合や普遍集合 (universe) などと呼ばれる（大きな）集合 U を固定して、その部分集合についてのみ考えているとき（例えば、U が自然数全体、実数全体やある位相空間であるときなど） U の部分集合 A について、
$\displaystyle U\smallsetminus A$

を A の（絶対）補集合（ほしゅうごう、complement）といい、Uが了解されている文脈では単に
$\displaystyle A^{\mathrm {c} },\,\complement A,\,{\overline {A}}$
などと表す。

・ある集合の補集合の補集合はもとの集合自身である。
・自然数について考えているとき、奇数全体の集合の補集合は偶数全体の集合である。
・実数全体 R について考えているとき、有理数全体 Q の補集合

$\displaystyle \mathbf {R} \setminus \mathbf {Q} $ は無理数全体である。
Wikipedia

例が挙げられているので分かりやすいですね。

補うの意味の通りで、ある集合のそれ以外の元を全て補集合と呼びます。

左図なら赤は全て補集合。

既述のように、偶数の補集合は全ての奇数です。

和集合

【和集合】
集合 A と集合 B が与えられたとき、集合 A ∪ B を、A, B いずれかの集合の少なくとも一方に含まれる元 x の全体 (x ∈ A ∪ B ⇔ x ∈ A または x ∈ B) として定めて、あるいは同じことだが
${\displaystyle A\cup B:=\{x\mid x\in A{\mbox{ or }}x\in B\}}$

として定義される集合を、集合 A, B の和集合と呼ぶ。
Wikipedia

ボクシングとキックボクシングを合わせて「立ち技競技」と定義するとかですね。

共通集合

集合 A, B の交わりは A ∩ B と記される^[4]。これはx ∈ A ∩ B ⇔ x ∈ A かつ x ∈ B

ということであり、記号ではA ∩ B = { x | x ∈ A∧x ∈ B }

と書ける。A ∩ B に含まれるような元が存在するとき A と B とは互いに交わるあるいは交わりを持つといい、そのような元の存在しないとき A と B は互いに素であるまたは交わりを持たない (disjoint) という。
Wikipedia

リビアヤマネコ（ヨーロッパヤマネコ）が家畜化されたイエネコに対する通称である。

「リビアヤマネコ」の集合と「家畜化された動物の集合」の共通集合がイエネコと呼ばれます。

次回やろうと思いますが、以上のように集合を定義から集合の持つ「ドモルガンの法則」といった定理（性質）を導き出すことができます。

ドモルガンの法則

【ドモルガンの法則】
P, Q をある集合の部分集合とするとき、

$\displaystyle {\begin{aligned}(P\cup Q)^{\mathrm {c} }&=P^{\mathrm {c} }\cap Q^{\mathrm {c} }\\(P\cap Q)^{\mathrm {c} }&=P^{\mathrm {c} }\cup Q^{\mathrm {c} }\end{aligned}}$
が成り立つことが分かる^[3]。
Wikipedia

PとQの和集合の補集合がPの補集合とQの補集合の共通集合にい等しく、PとQの共通集合の補集合がPの補集合とQの補集合の和集合である。
集合の足したり引いたりの演算を定義した場合に導かれる定理ですね。

これはもっと一般化できて、{P_λ}_λ∈Λ をある基礎となる集合の部分集合の族とするときに、

$\displaystyle {\begin{aligned}\left(\bigcup _{\lambda \in \Lambda }P_{\lambda }\right)^{\mathrm {c} }&=\bigcap _{\lambda \in \Lambda }P_{\lambda }^{\mathrm {c} }\\\left(\bigcap _{\lambda \in \Lambda }P_{\lambda }\right)^{\mathrm {c} }&=\bigcup _{\lambda \in \Lambda }P_{\lambda }^{\mathrm {c} }\end{aligned}}$
が成り立つ。これらをド・モルガンの法則という。
Wikipedia

【命題論理における法則】
任意の命題 $\displaystyle P,Q\in \{\bot ,\top \}$
に対して
$\displaystyle \neg (P\lor Q)=\neg P\land \neg Q\,,$
$\displaystyle \neg (P\land Q)=\neg P\lor \neg Q$
が成り立つ。これをド・モルガンの法則という^[1]
Wikipedia

$P \land Q$は論理和を表し、PまたはQが真なら命題の真理値は真になります。
$P\lor Q$は論理積を表し、PとQが真なら命題の真理値は真になります。

ドモルガンの法則は集合の定義から導かれる集合の性質で、このひな形に当てはめることで真偽の判定を簡略化できます。
議論が複雑化してぱっと見で分からなくなったとしても、とりあえずドモルガンの法則に当てはめてしまえば真偽は判定できます。

【例】
次の命題「私の身長は160cm以上であり、かつ私の体重は50kg以上である」

の否定、すなわち「「私の身長は160cm以上であり、かつ私の体重は50kg以上である」ではない」

は、ド・モルガンの法則によれば、次の命題と等しい。「私の身長は160cm未満である、または私の体重は50kg未満である」

同じようにして「このボールは青いか、または赤い」

の否定は「このボールは青くなく、かつ赤くない」

になる。
Wikipedia

【恒真式】
（こうしんしき、トートロジー、英: tautology、ギリシャ語のταυτο「同じ」に由来）とは論理学の用語で、「aならば aである (a → a) 」「aである、または、aでない (a ∨ ￢a)」のように、そこに含まれる命題変数の真理値、あるいは解釈に関わらず常に真となる論理式である。
対義語としては変数の値にかかわらず常に偽となる矛盾である。
Wikipedia

【矛盾】
・伝統的論理学で、二つの概念または命題が一定の事象を同一の観点から同時に、一方が肯定し他方が否定する場合の両者の関係。
・命題論理学で、複合命題からなる論理式の各要素命題にいかなる真理値を与えても必ず偽となる式。
Wikipedia

議論をする際には普通
「対象を固定」→「意味のある構造に分解」→「分解した構造の意味の細部を推察」→「それぞれの意味の関係について考える」「総体の意味を明らかにする」
という手順になると思います。
コンピューターであれば「演算装置」「記憶装置」「制御装置」「入力装置」「出力装置」という具合に分解でき、それぞれの役割を定義することで総体である「コンピューター」の動作原理を理解することができます。
人の脳の情報処理体系を考える場合も「大脳皮質」「○○野」「小脳」って具合に分解して、それぞれの役割を定義し、総体としての脳が何をしているのか確かめています。
いつの日かその二つを「生命」という意味において並べられる日が来るかもしれませんよね。

問題解決の際の問題の切り分け方で結論が異なってしまっては困りますから、厳密性を重んじる数学ではそれを防ぐための雛形が用意され、それ以外の方法を禁じているわけですね。

中学以上の数学は公式を覚えさせるのではなく、論理的な議論の組み立て方を教えるべきだと感じますね。公式を暗記するより遥かに社会で役立ちます。

最近、色々あって感情論に辟易しています。
それ自体を否定するつもりはないのです。
感情は大切です。理解しています。
だけど、法律的な論点を感情のそれにすり替えられて正当性を主張されてもこちらは譲歩しかねます。
「カウンセリングを受けてくれ」としか。