外積
外積
3次元実数空間 $\mathbb{R}^3$ において、2つのベクトル $\vec{a} = (a_1, a_2, a_3)$ と $\vec{b} = (b_1, b_2, b_3)$ が与えられたとき、その外積 $\vec{a} \times \vec{b}$ は以下の成分を持つベクトルとして定義されます。
$\vec{a} \times \vec{b} = \begin{pmatrix} a_2b_3 – a_3b_2 \\ a_3b_1 – a_1b_3 \\ a_1b_2 – a_2b_1 \end{pmatrix}$$
「垂直であること」の厳密な証明生成されたベクトル $\vec{c} = \vec{a} \times \vec{b}$ が、元の $\vec{a}, \vec{b}$ と垂直であることを確認するには、内積が $0$ になることを示します。$\vec{a} \cdot (\vec{a} \times \vec{b}) = 0$$\vec{b} \cdot (\vec{a} \times \vec{b}) = 0$
引用gemini
二つのベクトルが与えられた時、いずれとも垂直になるベクトルを生成するのが外積。
すなわち
$\boldsymbol{a}・(\boldsymbol{a}×\boldsymbol{b})=0$
$\boldsymbol{B}・(\boldsymbol{a}×\boldsymbol{b})=0$
になる規則を実現するのが外積であり、AIが教えてくれた演算規則。
※✕を外積、・を内積と仮定
$\boldsymbol{a}・(\boldsymbol{a}×\boldsymbol{b})=0$
$\boldsymbol{B}・(\boldsymbol{a}×\boldsymbol{b})=0$
になる規則を実現するのが外積であり、AIが教えてくれた演算規則。
※✕を外積、・を内積と仮定
以下はその意味を考える。
垂直なベクトルを取り出したいのは、ある二つの軸(要素)と無関係な軸(要素)を取り出したいから。
敷衍するなら、外積によって今までにない新たな視点が生まれる方向を定義したいから。
敷衍するなら、外積によって今までにない新たな視点が生まれる方向を定義したいから。
もっと現実的な解釈なら、例えば、回転などの動的な現象を2次元直交座標系で記述するとなると計算処理が膨大になってしまうから。計算量を減らしたいから。
直進する物体は軸に掴まえられると軸を支点に回転する(トルク参照)。
回転するフィギュアスケーターが腕を縮めて回転力を増大させるのに見覚えありませんか?
腕の曲げ伸ばしという横の動きが回転という別の次元に変換されています(外積)。本当にそうなっているかは置いといて、そうだと仮定すると計算が楽。
腕の曲げ伸ばしという横の動きが回転という別の次元に変換されています(外積)。本当にそうなっているかは置いといて、そうだと仮定すると計算が楽。
仮にフィギュアスケーターの回転力の増大を二次元直交座標系で記述しようとすると計算処理やその表現があまりにも煩雑になる。
そもそも回転力を表現するスペースがない。
そもそも回転力を表現するスペースがない。
よって新たな次元を作り出して回転を直線(ベクトル)に翻訳して記述することにした。
また、意味の直交=無関係、と解釈するなら論理的には、外積は二つのベクトルA,Bと無関係の意味を生じさせることとも対応させられる。
物理的な現象の記述においても、論理的な記述においても対応関係が作れて便利。
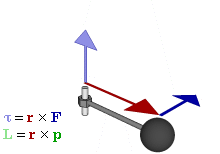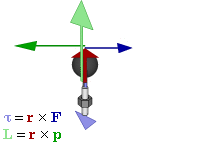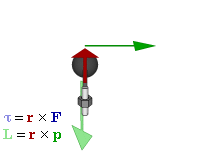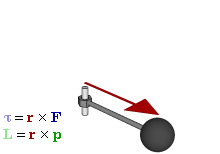
下のトルクのgifが分かりやすいと思う。
軸に固定した物体が直進すると、その力は回転力に変換される。
軸に固定した物体が直進すると、その力は回転力に変換される。
仮にその回転力をそのまま直交座標系で表現しようとすると計算と記述の作業があまりに煩雑になる。
論理的な意味であれば、商品価格を「価格と質」というトレードオフ関係から切り離して、「環境負荷」「サブスク」などという、新たな評価軸(意味)を生み出すようなこと。
※従属してる気がするから便宜上の表現として理解して
※従属してる気がするから便宜上の表現として理解して
つまり、二つの意味から生まれた新たな意味が、元の二つの意味との従属関係にあるのを避けたい場合に、すなわち、いずれとの内積も0となる方向を作りたい場合に外積が用いられる。
まとめ。回転とその広がりをそのまま直交座標で表現するとあまりにも処理が冗長になる、そもそもただの計算処理なのだから、あえて回転で表現する必要がない。仮に回転を直線に翻訳すればは計算処理が劇的に低下する。これが外積。
根本にあるのは、二つのベクトルの内積(関係性)が0(無)であってほしいという願い。


コメント