極限の定義を学びましたので、次にその定義から導き出せる極限の性質を学んでいこうと思います。
この世界はこうなっているだろうという公理を決め、その公理から導き出せる性質を元に世界を理解する論理を手に入れることが数学の目的です(長濱説)。
前回の極限の定義から導き出せる性質を学んでいきます。
極限の一意性
「限りなく近づいていく」のイメージから何となくある1点に数列の極限は収束していくような気はしますが、イメージは間違っている可能性は排除できないし、曖昧さを許さない数学では厳密にこれを証明しなければなりません。
「数列の極限が収束する場合、それは一つに定まる」という命題を確かめていきます。
一意性とはユニーク、それしかないという意味です。
αとβが同値であることを証明
極限の一意性を証明します。
収束先が二つある(α ≠ β)と仮定すると、極限はα,βは別々の2点に収束することになります。まずはそれを確かめる過程で、それが間違いであること、α = βが同値であるという論理を導き出します。
二点に収束するので、
$\displaystyle \lim_{n \to \infty} a_n = α$ (1)
$\displaystyle \lim_{n \to \infty} a_n = β$ (2)
となります。
極限がαに収束するためには、ε – N論法より$\vert a_n – α\vert < ε$が成立するような$n > N_1$が存在しなければなりません。
また同時に極限がβに収束するためには、ε – N論法より$\vert a_n – β\vert$ < εが成立するような$n > N_2$が存在しなければなりません。
二つの極限に収束すると仮定しているので、あるN(ε)を決めれば、それ以上の自然数nの範囲内では常に既述の二つの条件が満たされる必要があります。
つまり、$N_1,N_2$の内の大きな方を取れば常にαとβの両方に収束するわけです。
$N = \max(N_1,N_2)$
$n > N ⇒ \vert a_n – α\vert < ε, \vert a_n – β\vert$ < ε$
maxは大きい方を取るという意味の記号なので、$N_1,N_2$の大きい方がNになります。
また条件より
$\vert a_n – α\vert + \vert a_n – β\vert < 2ε$
が求められます。
ε以下のものを足した場合、2εは超えませんよってことです。
ここで突然ですが、こんな式を作ります。
条件の登場人物から導き出せる式です。
$\vert α – β\vert = \vert(α – a_n) + (a_n – β)\vert$
$a_n$が打ち消し合うので意味は変わりません。
この式を使って下のような不等式が作りだせます。
これは後程補足しますが、絶対値の性質を利用しています。
$\vert α – β\vert= \vert(α – a_n) + (a_n – β)\vert \leqq \vert a_n – α\vert + \vert a_n – β\vert < 2ε$
完成しました。
後はこの式の意味を読み取ります。
2εより小さく、$\vert a_n – α\vert + \vert a_n – β\vert$よりも小さな$\vert α – β\vert$の値はεを小さくしていけば、それに応じて限りなく小さくなっていくことが示されています。
そして、$\vert α – β\vert$とはαとβの差のことなので、αとβの差が限りなく小さくなる、つまりαとβが同じ値に収束することを示しています。
定義から導き出した不等式より、α≠βは成立せず、常に同じ値に収束することが示せましたので、極限が一点に収束することが証明できました。
補足:
$\vert(α – a_n) + (a_n – β)\vert \leqq \vert a_n – α\vert + \vert a_n – β\vert$
この部分は絶対値の性質です。
まだ証明していません。
今回、この証明は面倒なのでこの不等式の形は正しいと認めてしまいました。
必要なら別で絶対値の定義を確認し性質を証明していきます。
今は極限にやる気を出しているので、他はやる気が起きないだけです…
α≠βが成立しないことを証明
今度は三角不等式による背理法で証明していきます。
背理法
コトバンク
命題の仮定のほかに,結論の否定を仮定して推論を行ない,そこから導かれる矛盾を示すことで命題を証明する方法。 帰謬法(きびゅうほう)とも呼ばれる。 数学における重要な証明方法の一つである。
α ≠ βでは矛盾が生じることを証明し、α = βであること証明する。
三角不等式
Wikipedia
任意の三角形に対してその任意の二辺の和が残りの一辺よりも大きくなければならないことを述べるものである[1][2]。

三角形の二辺の和より残りの一辺は小さいよねってこと。
三角不等式の証明もまた今は面倒なので正しいと認めてイメージで理解してしまいます。
それでは証明していきます。
α ≠ βと仮定しているので$\vert a_n – α \vert,\vert a_n – β \vert ,\vert α – β \vert$の関係には三角不等式
$\vert a_n – β \vert < \vert a_n – α \vert + \vert α – β \vert$
が成立します。
$\vert a_n – α \vert$はε以下なので置き換えると
$\vert a_n – β \vert < ε + \vert α – β \vert$
この式から分かることは$a_n$がβに収束するためには$\vert α – β \vert$が0でなければなりません。
α ≠ βが成立しfません。
裏を返せばα = βであるということです。
補足
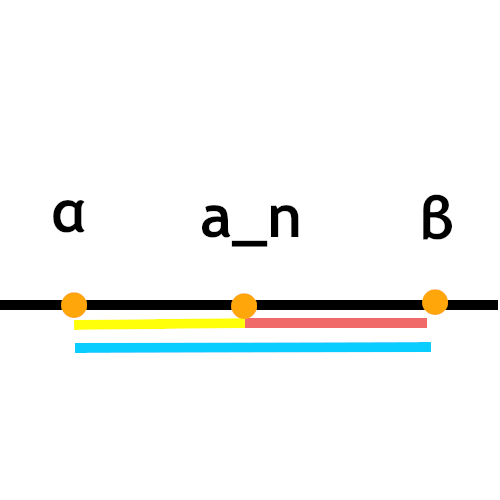
$\vert α – β \vert$は青の直線、$\vert a_n – α\vert$は黄色の直線、$\vert a_n – β \vert$は赤の直線。
三角形を上から押しつぶしたような形だと考えてください。
絶対値とか三角不等式で使ったような論理は数学だとよく見る気がしますね。
そのほかにも
$\displaystyle \lim_{n \to \infty}a_n = α$
$\displaystyle \lim_{n \to \infty}b_n = β$
が成立する時に
$α + β = \displaystyle \lim_{n \to \infty}(a_n + b_n)$
$αβ = \displaystyle \lim_{n \to \infty}(a_nb_n)$
$\frac{α}{β} = \displaystyle \lim_{n \to \infty}(\frac{α}{β})$
$α > β$なら$a_n > b_n$
という性質がありますが今は証明が面倒なので飛ばします。
極限の性質で詰まったらやります。
ある値に収束するなら、普通の数のように四則演算とか不等式が使えるよってことですね。



コメント