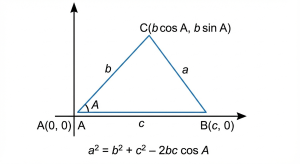
余弦定理の導出

数学とか

2025.12.22

余弦定理

単位円の性質
$1^{2}=cos^{2}Θ+sin^{2}Θ$

$a^{2}=(bcosA)-c^{2}+b^{2}sin^{2}A$(①と三平方の定理)
$a^{2}=b^{2}cos^{2}A-2bccosA+c^{2}+b^{2}sin^{2}A$(展開公式)
$a^{2}=(cos^{2}A+sin^{2}A)b^{2}+c^{2}-2bccosA$(分配法則)
$a^{2}=(1)b^{2}+c^{2}-2bccosA$(①)
$a^{2}=b^{2}+c^{2}-2bccosA$(乗法単位元)

余弦定理完了。

頭の中で上の画像の頂点Cから垂線を下ろして直角三角形を二つ作ってください。三平方の定理を知っていればあとは何となく分かるはず。