実数の性質→単調増加数列の性質→区間縮小法の流れで「ボルツァーノ=ワイエルシュトラスの定理」という二人の偉人が証明した定理を見ていきます。
ボルツァーノ=ワイエルシュトラスの定理
有界な実数集合内にある数列は収束部分列を持つ。
$\forall ε,\exists K \in \mathbb R;k \geq K \Rightarrow \vert a_{n(k)} – α \vert < ε$
「部分列が収束する」の前に「部分列」が分からないのでまずはここから。
ボルツァーノ=ワイエルシュトラスの定理
部分列
部分列はある数列の数を順番を変えずに抜き出した数列です。
例として$(-1)^n$を挙げます。
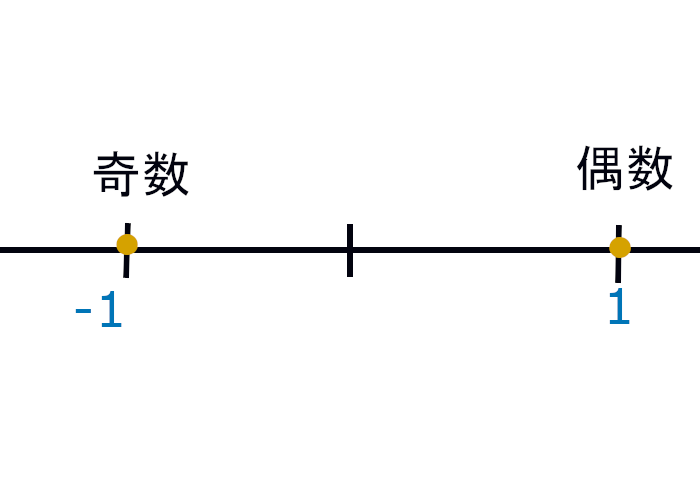
$(-1)^n$は偶数と奇数で別々に分布しています。
この数列を偶数部分、奇数部分に分解したのが部分列です。
$(-1)^n$は行ったり来たりするだけなので、部分列を抜き出すとそれぞれ1と-1に収束します。
n = 偶数だと1にn = 奇数だと-1に。
これを証明しようってことです。
部分列の表記
数列は$a_1,a_2,a_3…$と表しましたが、部分列を表す場合は$a_{n(1)},a_{n(2)},a_{n(3)}…$と表現されます。また$a_n \leq a_{n(n)}$になります。
順序良く間引いていくので元の数列の添え字nを大きくすれば、同時に部分列の添え字も大きくなっていきます。
それでは「部分列は収束する」を前回証明した区間縮小法によって証明します。
と言っても証明というよりは言い換えているだけです。
区間縮小法の簡単な復習をします。
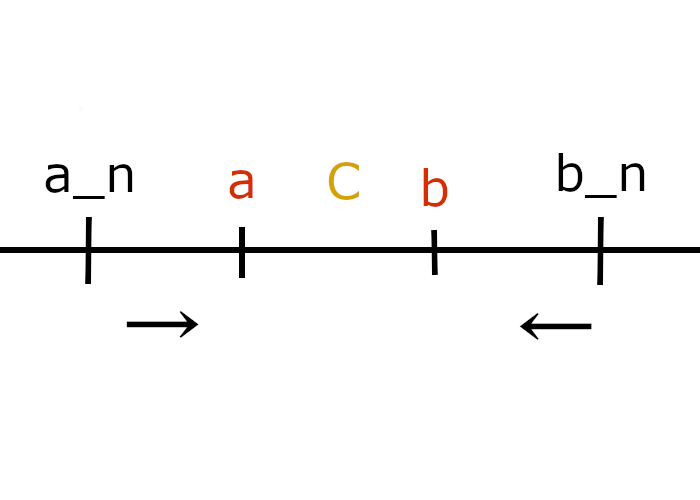
「集合Iの両端をどんどん縮めていけばある一点に収束するよね」という主張です。
$a_n,b_n$を縮めて収束点であるa,bに限りなく近づけていった場合a – b = 0の時にa = b = cになり、集合Iはその元Cに収束すると言えます。
この区間縮小法を使って証明していきます。
Wikipediaから引用します。

上界S下界sの集合を定義します。
$X_n$は$I[a_1,b_1]$に存在する無限の数列です。

Iに中点$I_1 = \frac{\vert a_1 – b_2 \vert}{2}$をつけます。

半分に分割された数列の中から無限に存在する方を選びます。どちらも無限に存在する場合はどちらでも構いません。
元の数列が無限なので、論理的に少なくともどちらかは無限になります。
※有限 + 有限 = 有限

半分にした区間ををさらに半分にする$I_2 = \frac{a_2 – b_2}{2}$を設定します。

分割した区間の無限にある方をまた分解して$I_3$を決めます。

この処理を無限に繰り返すと区間の幅は限りなく0へ近づきます。
また数列は無限に存在する方を選び続けるので、限りなく小さな区間にも点が存在しています。よってε – N論法により極限をとるとある一点に収束すると言えます。

上記のように$I \supset I_1 \supset I_2 \supset I_3…$って感じで部分集合をとっていく時に部分集合の中から一点、図の黄色の点を選んでしるしをつけていきます。
その点にそれぞれ$a_{n(1)},a_{n(2)},a_{n(3)}$と自然数を順番に割り当てて名前を付ければ部分列の出来上がりです。
区間縮小法により$\displaystyle \lim_{n \to \infty} a_n = b_n = C$となり、$C \in I_n$なので部分列$a_{n(k)}$もε – N論法により収束すると言えます。
※表記の方法が間違っているかも
この証明は解析学では非常に大きな役割を果たすそうなんですが、今の僕にはその具体的な例が想像もできません。
ただ何となく、無秩序な数列を秩序ある複数の部分列に分解することができれば、その部分列を眺めていくことで、一見して無秩序に見えた数列の中の法則を見出すことができるのかなあって思いました。


コメント