人の認識を延長したものが含意、さらにその含意を延長し集合を含む概念にしたのが写像、関数。
この文脈から自然数の定義にどんな物語が与えられるのかを見ていきます。
人の認識って文脈から数学を理解しようって試みであくまでも長濱説、我流です。
写像と含意と認識
認識はあることが成立するための因果関係です。
「あれは椅子である」という認識は椅子を成立させるいくつかの前提(原因)から演繹される判断(結果)です。
必要条件と十分条と集合
因果関係を表す認識の定義として必要条件と十分条件があります。
図にすると分かる通り、ある集合を満たせば、それに包含される集合の条件も自働的に満たされるような構造をしています。
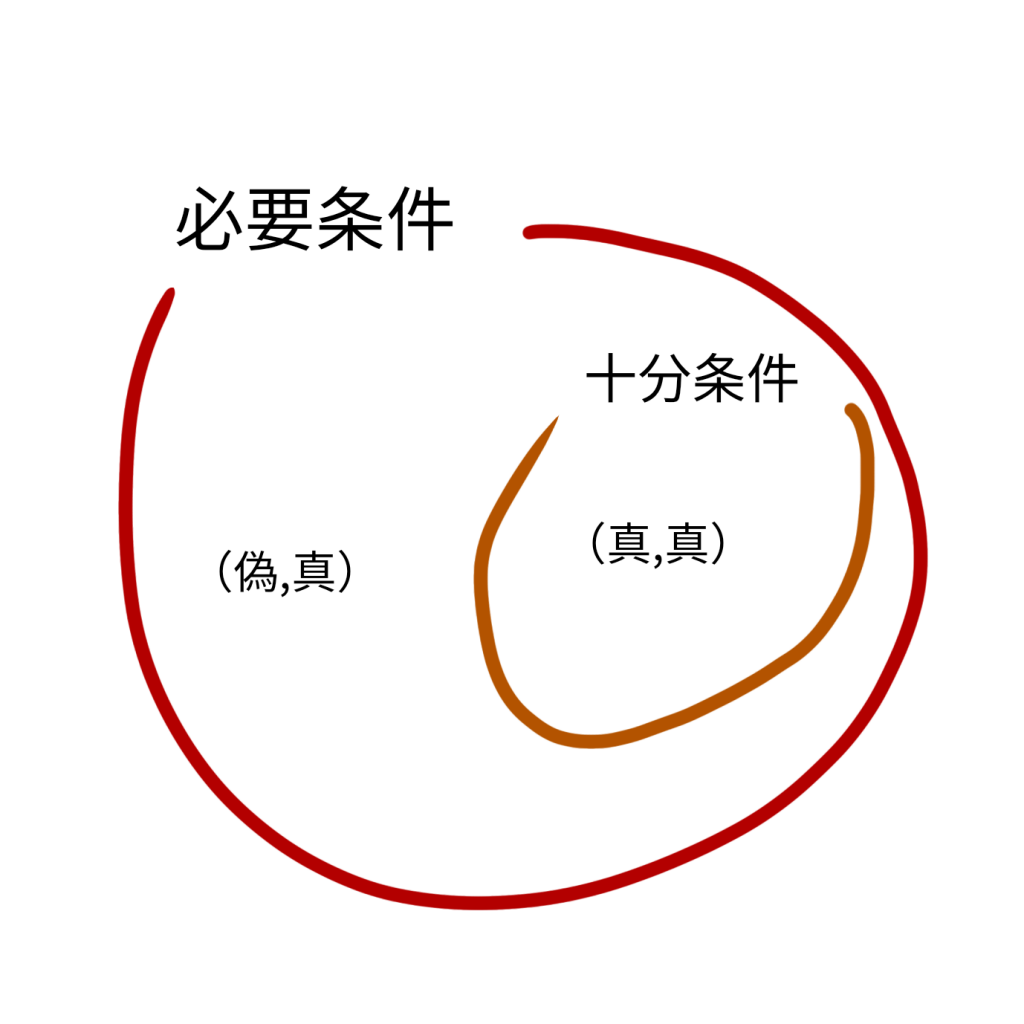
「人」は「動物」という条件(集合)を包含しているので、「人」という条件を満たせば「動物」という条件も必然的に満たされます(十分条件)。
「動物」に情報を付け加えて「人」が定義されるので「動物」の方が情報量が少なく、「人」の方が情報量が多くなります。
これが集合が誕生する文脈だと思います。
「あれは犬である」という推論が真である場合、「牙」「四足歩行」「毛」といった犬という集合の要素(前提)が真であることを意味します。
これは
前提(原因)→結論(結果)
という人の認識を言語化した形です。
あくまでも人の認識の範疇でしかありません。他の恒星系に住む宇宙人がそうとは限りません。別次元人の住人や神はこんな認識はしないと僕は思います。人は人の認識が限界になっていて、現時点では観測的な整合性がとれていますが、どこかの領域から何も分からなくなってしまう気がするんですよ。
宇宙の始まりや存在、非存在の境界線など。宇宙は「最初からあった」なら原因はありませんし、「何かから生まれた」なのだとしたらその前は?その前は?その前…と堂々巡りが無限に続きます。
閑話休題。
人の認識という文脈から自然数とはどのような認識なのかを見ていきます。
自然数の定義の認識
【自然数の定義】
Wikipedia
自然数 1 が存在する。
任意の自然数 a にはその後者 (successor) の自然数 suc(a) が存在する(suc(a) は a + 1 の “意味”)。
異なる自然数は異なる後者を持つ。つまり a ≠ b のとき suc(a) ≠ suc(b) となる。(ある種の単射性)
1 はいかなる自然数の後者でもない(1 より前の自然数は存在しない)。
1 がある性質を満たし、a がある性質を満たせばその後者 suc(a) もその性質を満たすとき、すべての自然数はその性質を満たす。
ややこしいですが簡単に要約すると。
1を起点として定義する→1を後者関数に入力しその出力を後に続く後者と定義する→さらにそれを入れ子にする…と言う風に延々と自然数を創り出す作業が定義されています。最後に数学的帰納法を定義しています。
1 or 0は旧約聖書で言うところの「主(神)」です。物語の起点として必要になる絶対的な存在で、神(0)との関係を定義することによりその後の登場人物、物語の意義が定義されていきます。
【自然数の加法】
Wikipedia
自然数の加法は再帰的に、以下のように定義できる。
すべての自然数 a に対して、a + 0 = a
すべての自然数 a, b に対して、a + suc(b) = suc(a + b)
Wikipediaの自然数の加法の定義は0で定義されていますが、1でも同じような論法で定義できます。
まず起点となる0と他の自然数の加法の関係について明らかにし、次に後者関数により0ではない自然数同士の加法について定義されています。
0ではない加法の定義も下記のような形に定義し直されるので、結局は0との関係によって加法は定義されていると言えます。
2+3=s(s(0))+s(s(s(0)))=s(s(s(s(s(0)))))
「2+3は0の後者の後者の後者の後者の後者」。
以上自然数は後者関数の入れ子、つまり認識の入れ子構造になっていることが分かります。
【自然数の乗法】
Wikipedia
加法が定義されたならば、自然数の乗法は再帰的に、以下のように定義できる。
すべての自然数 a に対して a × 0 = 0
すべての自然数 a, b に対して a × suc(b) = (a × b) + a
これも結局は加法、つまり0との関係により定義されているので、それはつまり因果関係の認識の入れ子構造だと言えます。
=は同値で同値は反射率、推移律、対称律により定義され、それは含意を拡張した形になっています。これも人の認識です。
今回は疲れたのでこれで終わります。



コメント