群の分野の続きです。
自然数
頭では群を抽象化し厳密に定義することの意味は理解できていますが、その威力を体感していないので、なんだか群の輪郭がぼやけています。
というわけで簡単に群にはどんなものがあるのか見ていきます。
定義
群の定義を簡単におさらいすると
「群Gの元(げん)の演算の結果は群Gを写していなければならない(閉性)」
「演算の順序によって結果が変わってはならない(結合法則)」
「単位元が存在しなければならない」
「逆元が存在しなければならない」
です。
具体的には以下の記事で。
可換群
$x,y \in G,x \cdot y =y \cdot x $が成立するような群は「可換群(アーベル群)」と呼ばれます。
行列は可換群の定義は満たしません。
補足
群の元の数を位数と呼び。
$|G|$と表します。
数の世界の群
上記の定義通りに数の世界を見てみます。
自然数
自然数の集合$\mathbb N$が群であるかどうか。
まずは自然数の演算が自然数を写す写像なのか(閉性)を確認してみます。
$G \cdot G = \longmapsto G$
そのためには自然数の加法が定義を満たしているのかを知れば良いですね。
自然数の加法の定義を見ていきます。
自然数の定義
自然数の定義は公理です。
これは証明不可能だから認めてしまおうって世界観です。
自然数 1 が存在する。
任意の自然数 a にはその後者 (successor) の自然数 suc(a) が存在する(suc(a) は a + 1 の “意味”)。
異なる自然数は異なる後者を持つ。つまり a ≠ b のとき suc(a) ≠ suc(b) となる。(ある種の単射性)
1 はいかなる自然数の後者でもない(1 より前の自然数は存在しない)。
1 がある性質を満たし、a がある性質を満たせばその後者 suc(a) もその性質を満たすとき、すべての自然数はその性質を満たす。
Wikipedia
※0をはじめの数とする流儀もあるようです
空集合を
$0: = \emptyset = \{\}$
任意の集合 a の後者は a と {a} の合併集合として定義される。
5行目は数学的帰納法が成立することを要請しています。
翻訳すると「何か(例えば1)を起点を決めたらその後者はすべて決まった順序で並べられていて、起点が持つ性質はその後者にも全て受け継がれる。1の前には何も存在していない」
起点がないとだめで、循環していたり、枝分かれしていたり、飛ばし飛ばしではだめです。
ある起点からの一本道です。
合併集合は義務教育でやった和集合の別名です。
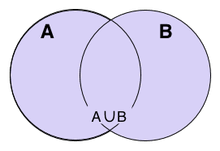
合併集合
コトバンク
2つの集合 A と B があるとき,A または B のいずれかに含まれるすべての元から成る集合を A ,B の合併または結び (結集合) といい,A∪B で表わし,A 結び B ,A ジョイント (またはカップ) B と読む。
加法の定義
ざっくりいきます。
すべての自然数 a に対して、a + 0 = a
Wikipedia
すべての自然数 a, b に対して、a + suc(b) = suc(a + b)
1行目は「加法の演算で0は何もしない(単位元)」2行目はsuc関数の変換方法を決めています。
「任意の自然数aには常に後者がある」「異なる自然数は異なる後者を持つ」の定義と数学的帰納法から自然数同士の加法が常に自然数を写す写像で、また閉じていることが言えます。
見方を変えると
「どんな自然数でも『S(S(S(0)))』て風に後者関数を重ねれば表現できるよね。で、0は自然数なんだからその後者は自然数だよね。だったらその後者も自然数で、その後者も….」
※S() = suc()
と言っていると解釈できます。
例えば1+3を考えます。
1 + 3 = S(0) + S(S(S(0))) = S(S(S(S(0 + 0)))) = 4
なんか屁理屈こねる小学生みたいな論法なんですけど、論理的には正しいです。
これをかっこよく表記すると上の定義になるんですけど、小学生でもわかる日本語に翻訳すると上記のようなくどい日本語になります。
減法の場合、例えば1-4だと自然数を写さないので群の定義に当てはまりません。
次に乗法の定義。
乗法の定義
加法が定義されたならば、自然数の乗法は再帰的に、以下のように定義できる。
Wikipedia
すべての自然数 a に対して a × 0 = 0
すべての自然数 a, b に対して a × suc(b) = (a × b) + a
1行目は「どんな自然数でも0との乗法は全て0になる」2行目は「自然数の乗法において後者関数は足し算に変形できるよ」です。
乗法は加法を省略した演算なので上の論法が通用します。
2 × 2 = S(S(0)) + S(S(0)) = S(S(S(S(0 + 0 )))) = 4
0の後者の後者の後者の…って論理なのでこの演算は閉じています。
自然数は群か
群の定義は加法に関しては成立しますが、減法についてはしません。
また0を含めた場合は0が単位元になりますが、含めない場合単位元はないので、0を含めた場合だけ群になります。
加法は逆元もありません。
乗法に関しては1が単位元になり、自然数は同士の乗法は自然数になるので定義を満たします。
結論、自然数は加法では0を含めた場合は群で、そうでない場合と演算の結果がマイナスになる可能性のある減法では群ではない。
乗法では群になる。
単位元と逆元を持たない構造のことを半群と呼ぶようです。
群のイメージが全然出来上がってないんですけど、こんなものなんですかね。
数学者は直観的に群かそうでないか分かりますか。
もう少し理解を深めるために今度は有理数とか実数で群について考えてみようと思います。





コメント