e = 2.71828 18284 59045 23536 02874 71352 …
ネイピア数はこんな定数です。
円周率と同じく無理数。
ネイピア数はヤコブ・ベルヌーイが複利計算をしている最中に発見しました。
銀行に金を預けると預けた額に数%付加されて返ってくるじゃないですか。
例えば年利が3%の預金口座に100万円を預けたなら1年後に103万円かえってくる計算です。
で、悪知恵の働くベルヌーイはこう考えました。
「預けた100万円を翌日、利息と一緒に引き出そう。そしてもう一度、今度は利息分も一緒に預けよう。これを毎日繰り返えせば、利息の分だけ運用額が毎日膨らんでいくぞ」と。
さらにベルヌーイは「もしかして毎秒引き出して毎秒預金したら、利息分だけ無限に金が生み出せるんじゃね!?錬金術だ!よっしゃ!銀行に行く前にいくらになるか計算してみよ!」と運用額がいくらになるのかを計算することにしました。
死闘の末に導きだした結果は
2.71828 18284 59045 23536 02874 71352 …
このラインが天井になり、これ以上は運用額が大きくならないことが分かりました。
上限ネイピア数に収束していきます。
ベルヌーイは「無限に増やせる錬金術ではないのか…」と肩を落としました。
全てを繋げる公式
しかしこのベルヌーイが発見したネイピア数、数学の様々な場面で登場するんです。
稀代の天才オイラーの導いたこの等式。

幾何学、解析学、代数学の分野でそれぞれ独立に定義された三つの定数 (π, e, i) がこのような簡単な等式で関連付いている。
Wikipedia
起点である0を形作るのは、『ネイピア数』『円周率』、自乗すると-1になる虚数、1、加法、指数。
数学の空間に存在する概念が結びつけられているんです。
オイラーの等式が今は何を意味しているのかは分かりません。
しかし、この非常にシンプルな等式は何かこの世界の本質を表しているように感じるんです。
ネイピア数の導出
何故自然対数の底(ネイピア数)なんてわけの分からない定数が生まれたのか。
結論から言うと自然対数の底を定義すると微分が便利になるんです。
まずは大切な定義から確認します。
定義
x = 0 の接戦の傾きが1となるような$y = a^{x}$の底。
言葉にするとこんな感じ。
式にすると。
$e = \displaystyle \lim_{h \to ∞}(1+\frac{1}{h})^{h}$
$e = \displaystyle \lim_{h \to 0}(1+h)^{\frac{1}{h}}$
$\displaystyle \lim_{h \to 0}{\frac{e^{x}(h -1)}{h}} = 1$
上の二つは「1とほんの僅かな数を∞乗したものがネイピア数ですよ」
どうやって奇妙な形のネイピア数へたどり着いたのか
どんな風にネイピア数なんてものを思いついたのか、人情としてはそこが気になりますよね。
ネイピア数の近似値と言えるものが記された最も古い文献は、1618年、ジョン・ネイピアによって発表された対数の研究の付録に収録されていた表である
Wikipedia
歴史を400年も遡るとこのテーマだけで年が明けてしまいそうなので、昔の人達の出発点はここだったんじゃないか?と勝手に推察して始めていきます。
自然”対数”の名が示す通り対数が関係していることは予想できます。
そしてネイピア数の定義が極限をとっていることから、出発点は恐らく「対数の微分」だったでしょう。
対数を微分していけば何か分かるかもしれません。
対数を定義通り微分していきます。
曲芸的な式変形を伴うので混乱しますが、基本的には対数の変換公式だけを利用しますので、簡単です。
微分の範囲はまだ扱っていませんが、ひとまず進めていきます。
まずは対数を微分の定義式に当てはめます。
$\displaystyle \lim_{h \to 0}\frac{log_{a}({x + h}) – log_{a}{x}}{h}$
hを外に出して見やすく整理。
$=\displaystyle \lim_{h \to 0} \frac{1}{h} log_{a}({x + h}) – log_{a}{x}$
この変換公式を使って対数の引き算を分数の形に変形。
$log_{a}{\frac{M}{N}} = log_{a}{M} – log_{a}{N}$
$=\displaystyle \lim_{h \to 0} \frac{1}{h}log_{a}{\frac{{x + h}}{x}}$
式の意味は変えず、分数の表現方法を変えます。
$=\displaystyle \lim_{h \to 0} \frac{1}{h}log_{a}{(1 + \frac{h}{x})}$
$\frac{1}{h} = \frac{1}{x}\frac{x}{h}$
なので
$=\displaystyle \lim_{h \to 0} \frac{1}{x}\frac{x}{h}log_{a}{(1 + \frac{h}{x})}$
に無理やり変形。
$log_{a}{M}^r = rlog_{a}{M}$
この変換公式を使って式を変形、$\frac{x}{h}$を肩に乗せます。
$=\displaystyle \lim_{h \to 0} \frac{1}{x}log_{a}{(1 + \frac{h}{x})}^{\frac{x}{h}}$
このままだと少し見づらいので$\frac{h}{x} = h\prime$と置きます。
$\frac{x}{h}$は$\frac{h}{x}$の逆数なので$\frac{1}{h\prime}$と表現できます。
$=\displaystyle \lim_{h \to 0} \frac{1}{x}log_{a}{(1 + h\prime)}^{\frac{1}{h\prime}}$
$\displaystyle \lim_{h \to 0} log_{a}{(1 + h\prime)}^{\frac{1}{h\prime}}$
出てきましたネイピア数の定義式らしきもの。
0へ飛ばすと()の中は1へ収束、指数部分は∞へ発散します。
この後の処理のために
$e = \displaystyle \lim_{h \to 0}(1 + h\prime)^{\frac{1}{h\prime}}$
とおきます。
対数の定義式を微分して得られた
$=\displaystyle \lim_{h \to 0} \frac{1}{x}log_{a}{(1 + h\prime)}^{\frac{1}{h\prime}}$
の底aを定数eとおくと
$= \displaystyle \lim_{h \to 0} \frac{1}{x}log_{e}{e}$
$log_{e}{e} = 1$
なので
$= \displaystyle \lim_{h \to 0} \frac{1}{x}\cdot1$
となります。
さらに×1は必要ないので省略すると
$= \displaystyle \lim_{h \to 0} \frac{1}{x}$
$\frac{dy}{dx}log_{e}{x} = \frac{1}{x}$
自然対数の微分の定義式が出てきました。
自然対数の微分てこんなシンプルな式でできてしまうんです。
さらにネイピア数の利用できる範囲を拡張していきます。
対数関数から指数関数へ
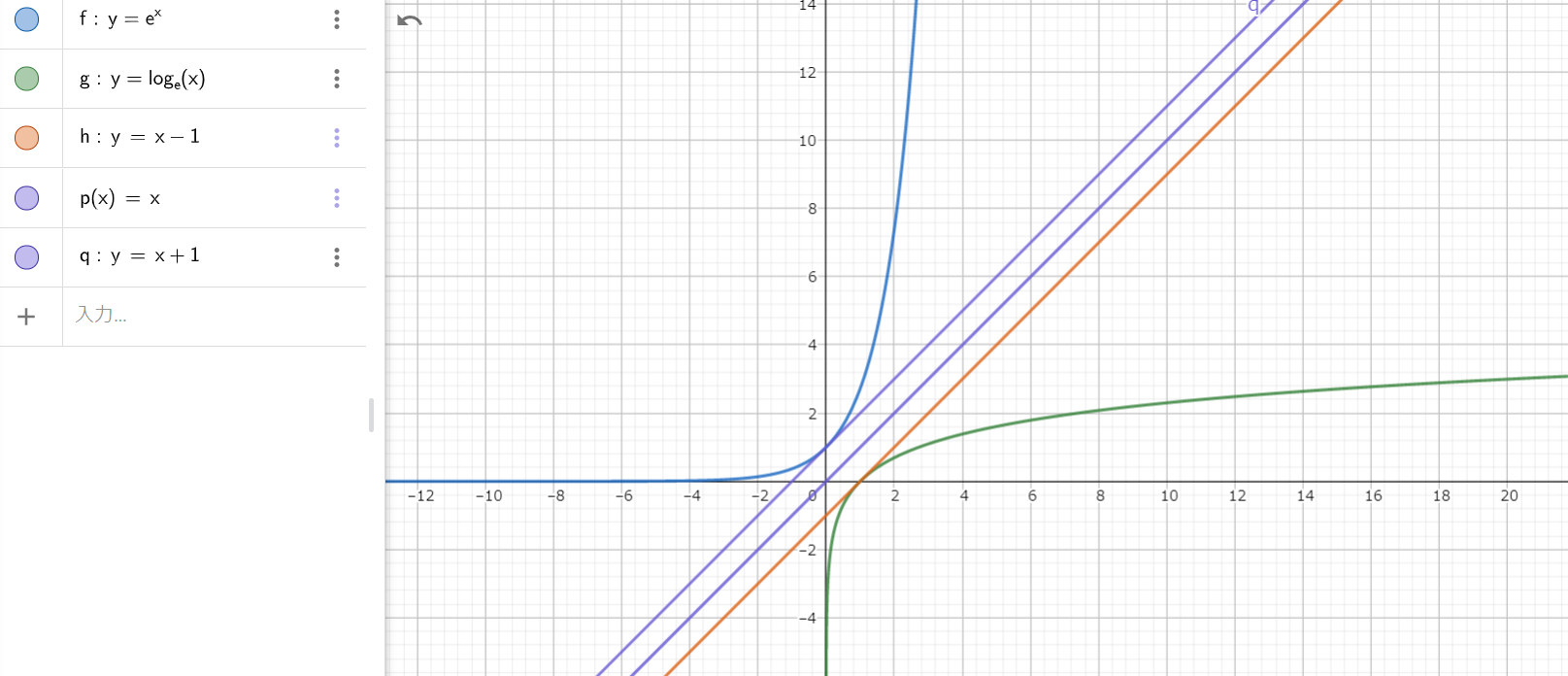
さて、以下のグラフは今回解説している対数$y = log_{e}{x}$(緑)と、それの(1,0)の接戦です。
$y = x – 1$の直線は$y = log_{e}{x}$を(0,1)で微分した時の接戦でもあります。
$y = log_{e}{x}$を(1,0)で微分すると傾きが1になります。
実際に自然対数の導関数に座標を当てはめて傾きを求めてみても
$\frac{dy}{dx}log_{e}{x} = \frac{1}{x}$
$\frac{dy}{dx}log_{e}{x} = \frac{1}{1}$
$\frac{dy}{dx}log_{e}{x} = 1$
以下のグラフ通りですね。
対数と指数の関係性を思い出してみると、対数の微分で登場したネイピア数eは指数にも適用できると予想できます。
そして、やってみたくなりますよね。
$y = log_{e}{x}$は「eをxにするにはy乗する」でした。
これをそのままを指数に変換すると$x = e^{y}$「eをy乗するとxになる」。
x = の式は気持ちが悪いですね。
なのでxとyの位置を交換して$y = e^{x}$に直します。
この式は上の式の青い曲線です。
$e^{x}$は$log_{e}{x}$の逆関数であるという性質も利用します。
※逆関数については今後やっていきます。
逆関数は原点を通る紫色の$y = x$の直線で線対称となります。
線対称なので原点を通る直線と微分して得られた紫色、オレンジの直線は並行になります。
つまり、$\frac{dy}{dx}e^{x} $の傾きは1。
逆関数は座標のxとyが入れ替わるので、接点は(0,1)。
論理的には$a^{x}$を(0,1)で微分した時の微分係数が1になるaの値はeであることを意味します。
微分の定義式で導いてみます。
$\frac{d}{dx}a^{x} = \displaystyle \lim_{h \to 0}{\frac{a^{x+h} – a^{x}}{h}}$
指数関数の変換公式$a^{m+n} = a^ma^n$を利用して$a^x$でくくります。
$=\displaystyle \lim_{h \to 0}{\frac{a^{x}(a^{h} -1)}{h}}$
$a^x$は定数なのでlimの外へだして
$= a^x\displaystyle \lim_{h \to 0}{\frac{a^h -1}{h}}$
$a^x$の導関数はこうなります。
出来上がった
$= a^x\displaystyle \lim_{h \to 0}{\frac{a^h -1}{h}}$
この式は
$ \displaystyle \lim_{h \to 0}{\frac{a^h -1}{h}} = 1$
になってくれると微分した前後で式の形が変わらないので使い勝手がよさそうです。
そうなるように変形していきます。
$ \displaystyle \lim_{h \to 0}{\frac{a^h -1}{h}} = 1$
をa = ~の形に変形します。
両辺にhをかけて
$\displaystyle \lim_{h \to 0}{a^h -1} = \displaystyle \lim_{h \to 0}{h}$
1を左辺へ移行
$ \displaystyle \lim_{h \to 0}{a^h} = \displaystyle \lim_{h \to 0}{h} – 1$
両辺を$\frac{1}{h}$乗すると定数になるのでlimがはずれて
$a = \displaystyle \lim_{h \to 0}({h} – 1)^\frac{1}{h}$
ネイピア数の定義が求められました。
ネイピア数を定義することで対数、指数を微分すると前後で式が変わりません。
ネイピア数を定義することで微分の面倒な計算を省略することができるようになりました。
ネイピア数を底とした指数関数と対数関数の微分がシンプルな式で完結できるのは微分を多用する物理学者、数学者には非常にありがたいことみたいですよ。
一見すると奇妙な定数でもあるネイピア数なんですが、こうやって成り立ちから想像して、道を辿ってみると、違和感なくすっきりとした気持ちで前へ進むことができます。
便利なネイピア数
既述のようにネイピア数を底とする指数関$e^x$は微分しても変化しません。
そして、積分しても変化しません。
現代物理では微分と積分で記述されることがほとんどなので、微分しても積分しても変化しないという性質が非常に重要なのです。
対数は任意の底に式を変形できる変換公式があることを思い出してください。
$log_{a}{b} = \frac{log_{c}{b}}{log_{c}{a}}$
無理やりにでも上記の変換公式で対数の底をネイピア数にしてしまえば、複雑な微分計算処理を省いて負担が軽減できます。
微積分を簡略化する。ネイピア数の役割の一つです。



コメント