
上の記事の派生。
上の記事でのメモとして書き残した直感は「行列計算の添字の規則に着目すれば、煩雑な行と列の個々の演算操作を、行列全体を一つの構造として扱える作業に置き換えられるんじゃね?」というもの。
つまり、行列の煩雑な計算を添字操作に置き換えて圧縮したい。
行列の添字操作
行列乗法と内積
以下は直感を説明する部品。
2つのベクトル a = [a1, a2, …, an] と b = [b1, b2, …, bn] のドット積は下記のように定義される[1]。
$\displaystyle {\boldsymbol {a}}\cdot {\boldsymbol {b}}=\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$
行列乗法
n × m 行列 A と m × p 行列 B
$\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1m}\\a_{21}&a_{22}&\cdots &a_{2m}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\cdots &a_{nm}\end{bmatrix}}$
$\displaystyle B={\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1p}\\b_{21}&b_{22}&\cdots &b_{2p}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mp}\end{bmatrix}}$
$\displaystyle c_{ij}=\sum _{k=1}^{m}a_{ik}b_{kj}$
で与えられる n × p 行列
$\displaystyle AB={\begin{bmatrix}c_{11}&c_{12}&\cdots &c_{1p}\\c_{21}&c_{22}&\cdots &c_{2p}\\\vdots &\vdots &\ddots &\vdots \\c_{n1}&c_{n2}&\cdots &c_{np}\end{bmatrix}}$
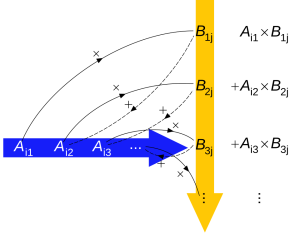
行列乗法の視覚化
ウィキ先生は本当に親切。分かりやすい画像まで。頻繁に利用してるなら募金しなきゃダメだよ。ウィキの思想は民主主義の土台だよ。

閑話休題。
視覚的に捉えると行列乗法はノイズが多すぎてスタックオーバーフローしてしまいます。そうだよね?
少なくとも、僕は4行4列とかになると1行1列の内積なんだっけ?となります。
内積と行列積の定義を「記号操作」として考えるなら、行列積は外側の添字を任意に固定して、内側のそれを一致させたまま実数の乗法と加法(内積)を進行させること。
ウィキの定義ならkを接着したまま動かすこと。

縮約
調べるとこれはアインシュタインが開発?した「縮約」という手法。曰く、相対性理論に並ぶ大発明※なんだとか。
※多分半分冗談だと思う
物理学なんて、情報の塊(=行列)を鬼のように処理するだろうから、煩雑な計算処理を記号操作として簡単化する縮約が大発明であることはなんとなく理解できる。
前回の記事で直感的にやった行列積の転置の変形を厳密にやります。
行列の添字の動きだけに着目します。
行列A,Bの乗法を仮定。
$\sum_{i=1}^{k} A_{ik}B_{kj}=C_{ij}$(行列積)
$C_{ij}^{t}=C_{ji}$(転置)
$C_{ji}=AB_{ji}$(行列積)…①
次にA,Bそれぞれの転置の行列積。
$A^{t}B^{t}=\sum_{i=k}^{n}A_{ik}^{t}B_{kj}^{t}=A_{kj}B_{ik}$(転置)
$A_{kj}B_{ik}=B_{ik}A_{kj}$(実数交換法則)
$\sum_{i=k}^{n}BA_{ji}$(行列積)
$\sum_{i=k}^{n}AB_{ji}$((実数交換法則)
①=②
前回記事では直感的にやりましたが、厳密化しても行列乗法の煩雑さを省略できる。
もっと便利な実例探してみよ。

コメント