白銀比

√2はどこにいるの無理数をやっているとたどり着く疑問。非循環な無限桁少数の位置はどう特定しているの？と。有理数は一つづつ規則的に変化させられる上に視覚的なグラフとしてそれを再現できるので、数直線上の位置を感覚的にイメージできます。2は...

連分数展開を練習していたら白銀比、白金比、黄金比という面白い数の話にたどり着きました。

これらは、身近な場所から宇宙観測まで、汎ゆる場所に現れる性質であるようです。

フィボナッチ数列で表されるようです。

確かに、フィボナッチ〜、という言葉は芸術からトレード、果ては宇宙まで、様々な場所で頻繁に出会います。

下の動画は、この世を支配している神のような黄金比の性質の一端を知ることができます。

比例式

そとそも、黄金比の「比」とは何ぞやと。

有理数定義引用WIIS

A : B = X : Y すなわち、二つの比 A : B と X : Y が等しいとは、B に対する A の割合が、Y に対する X の割合に等しいことであると定義すると、これはすなわち

$\displaystyle {A \over B}={X \over Y}$

なる分数の等式が成り立つことである。これは

$\displaystyle A:B=X:Y\iff {B \over A}={Y \over X}$

あるいは

$\displaystyle A:B=X:Y\iff {A \over X}={B \over Y}$

と定義しても同じである。このように定義される比の等式 A : B = X : Y あるいは分数の等式 A / B = X / Y を比例式という。

ウィキペディア

性質
x:y=m:n(仮定)
my=nx(有理数同値関係)
x:y=m:n→my=nx…①

連分数展開　√2の近似

無理数を小数で表現する方法の別の手法。今回は連分数で無理数を近似してみます。 √2の連分数展開まずは連分数で表せる形に√2を変形します準備1 $\sqrt{2}$(仮定) -1+\sqrt{2}$(加法逆元) +\sqrt{2...

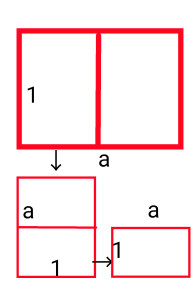
白銀比

白銀比

$\textstyle 1:{\sqrt {2}}$
の白銀比（はくぎんひ）は、1:1.414… で、約 5:7 である。紙の寸法などに用いられる。

ウィキペディア

長方形を半分に分割すると、二つの長方形が現れます。
分割してできた長方形の縦横比が分割する前の元の長方形の比と一致する長方形を考えます。

比が一致するので、①より
$1:a=a:2$(①)
と変形し
$a^{2}=2$(仮定)
$a=\sqrt{2}$(べき乗)

すなわち、そのような長方形の縦横比は1:√2となります。

これが白銀比です。
白銀比の長方形の紙を半分にすると、既述のように白銀比になります。つまり、どれだけ小さく折りたたんでも白銀比のままです。

証明
縦1横√2の長方形をきれいに半分に折った場合の比は
$1:\frac{\sqrt{2}}{2}$(仮定)
$\frac{1}{\frac{\sqrt{2}}{2}}$(比例式定義)
$\frac{2}{\sqrt{2}}$(逆元の逆元)
$\frac{2}{\sqrt{2}}･1$(乗法逆元)
$\frac{2}{\sqrt{2}}･\frac{\sqrt{2}}{\sqrt{2}}$(乗法逆元)
$\frac{2\sqrt{2}}{2}$(べき乗)
$\sqrt{2}$

短い辺の長さは1なので、白銀比をきれいに半分して作られる長方形は、どちらも1:√2となることが証明できました。

「白銀比の長方形を半分にすると白銀比になる」。つまり、白銀比は無限に現れます。

宇宙の至る場所に白銀比、黄金比、白金比が現れるのは、自己増殖、自己強化的な構造以外は宇宙は保存しないからでしょう。

無理数を規定している根源的な法則は何だろうか。ヒトには分からん？