集合の双対

上の我流で「双対関係」に文脈を与える試みの続き。
双対(そうつい、dual, duality)とは、互いに対になっている2つの対象の間の関係である。2つの対象がある意味で互いに「裏返し」の関係にあるというようなニュアンスがある(双対の双対はある意味で “元に戻る”)。
上の引用を手がかりに双対を考えます。
「存在」と「非存在」は、すなわち零次元の抽象的な空間においては、「在る」と「無い」の二つの関係が双対であると推理しました。この文脈なら零次元では1と0も双対です。
この視点でなら、∧と∨は一次元の認識であると解釈できます。
では、一次元の双対とは何と何であろうかと。
結論から言えば、それは「点」と「線」ではないかと。
始めは『「線」と「線ではない」』かなあ、と推理しました。しかし、これは抽象すると、「である」と「でない」の関係であると、つまりは上記の零次元の「存在」「非存在」と同義の関係の話であると気が付きました。
次に「線」と「点」が一次元の双対ではないか?と推理しました。
一次元において、他に表現可能な概念はそれらだけだと感じるから。
これを双対であるとするなら、一次元の双対は∧と∨で表現可能だと感じました。
∧=直線
∨=点
これは、ウィキペディアにある論理の双対関係とも一致します。
というわけで一次元の論理の双対は「線」と「点」であろうと結論して勝手に納得。
それらは下のような関係。
A∨Bの双対はA∧B。
A∨B(仮定)
¬(¬A∨¬B)(双対)
¬¬(A∧B)(ド・モルガンの法則)
A∧B(¬¬除去)
上は演繹を逆回転もさせられるので、逆も真の命題となります。すなわちA∧B、あるいはA∨Bの双対の双対はA∧BとA∨Bとなり、元へ戻ります。
この発想を延長すると「∃〜∀」も双対である、と導けます。
∧と∨へ∃∀を変換するなら
∃=(a∨b ∨c…)
∀(a∧b∧c…)
上の∧∨の双対関係へ変換可能、つまり∃∀は双対。とりあえずは納得して次へ。
次は包含関係の双対の文脈を推理します。
包含関係は⊂⇒。
A⇒Bは、AであることはBであることを含意、あるいはAはBを論理的に包含している、と言い換えられます。
⊂は部分集合。それは包含関係のこと。
⇒と⊂は図式化すると下のような感じ。
この包含関係の認識を規則化したのが「含意」の推論規則と言えます。
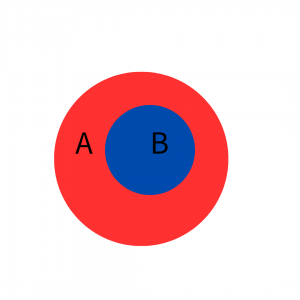
この関係の対は何だろうかと。
Aという命題の対は¬A
集合ならAの対はその補集合。
こう推理するなら
¬A→¬B
A^c⊂B^c
となります。
ただ、問題があり、それは仮にこれを⇒,⊂の双対とした問題は、包含関係が崩れてしまうこと。
包含関係を保つなら
¬B→¬A(対偶)
B^c⊂A^c
となります。
これが妥当な推理なら、二次元の包含関係における双対関係は
A→Bと¬B→¬A
A⊂BとB^c⊂A^c
これはウィキペディアの双対関係とも一致していますので、一先ず良しとします。これと不整合が現れたらなら、考え直します。
一先ずはこれで納得して今日は終わり。





コメント