
集合Aの部分集合とはすなわちべき集合とその濃度。
二つの要素を持つ集合のべき集合の要素数は
A=aがある
B=bがある
と定義すると要素の組み合わせは四通り
(A,¬B)(¬A,B)(¬A,¬B)(A,B)
べき集合の任意の要素xについては常に、「ある」か「ない」の二択なので、組み合わせは要素が一つ増えるごとに2倍、すなわち2^n個。
要素n個の集合Xのべき集合Yの要素数は
Y=|2^n|
集合Xの真部分集合Yは、そのべき集合から自分自身Y⊂Yを引いた集合なので
Y=|2^n-1|

y^2+1=(z-1)^2/(z+1)^2+1
=(z-1)^2/(z+1)^2+(z-1)^2/(z+1)^2
=(z-1)^2+(z+1)^2/(z+1)^2
=2(z^2+1)/(z+1)^2
1=(z-1)^2/(z+1)^2
と仮定。
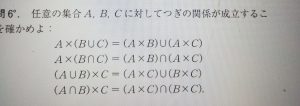
集合A,Bの直積集合A×Bは
Aの要素
a1,a2…an
とBの要素
b1,b2…bn
の順序対
(a1,b1),(a1,b2)…(a2,b1)(a2,b2)…
の全ての組み合わせ=分配法則①。
[A×(B∪C)](前提)
a∈A∧(b∈B∨C)(直積定義)
(A×B)∨(A×C)(①分配法則)
[A×(B∨C)→(A×B)∨(A×C)](→導入)
[(A×B)∨(A×C)](仮定)
(A×(B∨C))∨(A×(C∨B))(∨導入)
A×(B∨C)(べき等律)
[(A×B)∨(A×C)→A×(C∨B)](→導入)
[(A×(B∨C)→(A×B)∨(A×C))∧(A×B)∨(A×C)→A×(C∨B)](∧導入)
A×(B∨C)⇔(A×B)∨(A×C)(⇔定義)
A×(B∪C)⇔(A×B)∪(A×C)(∪定義)

上だけ。

U={U∈x|T}
Φ={U∈x|⊥}
x ∈U^c=x∉U
U^c(仮定)
¬T(補集合定義)
⊥(¬除去)
Φ(定義)
U^c→Φ
Φ^c(仮定)
¬⊥(定義)
T(¬除去)
U(定義)
Φ^c→U

A⊂B⇔A⇒B
⇒を推移律と仮定
A⊂B⇔A∩B
A∧B(⇔,除去
A∧B(∩同値変形)
A
A⊂B⇔A∩B→A
[A]
A∧A(べき等律)
A∩B(推移律)
A⊂B⇔A∩B(推移律)
A→A∩B⇔A⊂B(→導入)


[A∪B=Φ](前提)
∀x∈A∨∀x∈B=Φ(∪定義)
A→⊥(仮定1)
B→⊥(仮定2)
[⊥](∨除去)
A(⊥定義)
⊥→A(→導入)
A→⊥→A→⊥(推移律対称律反射律)
A⇔⊥(⇔定義)
⊥(前提1)
B(⊥定義)
⊥→B
B→⊥→B(推移律対称律反射律)
B⇔⊥(⇔定義)
A⇔B⇔⊥(推移律対称律反射律)
A∪B=Φ→A⇔B⇔⊥(⇔定義)

![]()
∃z∃y∀x∈ℕ(2x=y→2(x+1)=z)
∃z∃y∈ℕ(∀x∈ℕ((2x=y)→(2(x+1)=z)))
2a=b→2b+2=z
2a=b
b+1=z
∃x∀x∈ℕ(2x=y)→∃y∀x∈ℕ(x+1=y)
x=1
1×2=2
2×(1)+1=4

a
(A∩B)∪(A-B)(仮定)
(A∧B)∨(A∧¬B)(同値変形)
A∧B
A
A∧B→A
A∧¬B
A
A∧¬B→A
(A∧B)∨(A∧¬B)→A
A∧T
A∧(B∨¬B)
A→A∧(B∨¬B)
(A∧B)∨(A∧¬B)=A→A∧(B∨¬B)
b
A∪B=(A-B)∪B
A∪B
A∨B
(A∨B)∨¬B
A∨B∨¬B
A∨¬B∨B
(A-B)∨B
(A-B)∪B
A∪B→(A-B)∪B
(A∧¬B)∨B
A∨B∧¬B∨B
A∨B∨T
A∨B
A∪B
c
B∩(A-B)=Φ
B∧(A∧¬B)
A∧B∧(B∧¬B)
A∧B∧⊥
⊥
Φ

a
A⊂B
A-C
B-C
A-C→B-C
A⇒A-C→B-C
b
A⊂B
A⇒B
¬B⇒¬A
C-B
C∧¬B
C∧¬A
C-A

引用WIIS

コメント