集合論を進めていると「同値」って言葉が頻繁に出てきます。
a = b のことです。義務教育で習いましたよね。
日常生活でも何となく利用しているありふれた概念なので、深くその定義について考えてはいなかったのですが、ふと「そういえば『同値』って何…」って思いが頭に浮かんできました。
数学と人間の無意識
数学は問題が解決の手段
で、同値についてGoogleに聞いてみたら、それは「関係」を示すことなのだと説明してくれました。
「関係」も日常で頻繁に使う言葉ですが、厳密な定義なんて意識しませんよね。
だけど「『関係』を定義してみて」と言われたら難しくないですか。
僕が数学で面白いと感じるところは、この「AとBが関係している」というような、抽象的な概念を厳密化して、誰にでも納得のいく客観的な方法で議論できることです。
数学の公理が正しければ、ありとあらゆる問題は数学で解決できます。
話を「関係」に戻します。
数学的に、つまり論理的に「関係している」か「関係していない」かを議論するには、議論の対象に「直積集合の部分集合」が定義できるかを調べればいいのです。
「関係」って概念を「直積集合」「部分集合」という二つの概念を使って説明するので、なんだかヤバそうなきがしますよね。
だけど大丈夫、心配しないでください。
手続きを追えば難しくありません。
無意識のポテンシャル
関係という概念を僕らは日常的に使っています。
それはつまり、それが抽象的だったとしてもその意味を無自覚に定義していることを意味します。
明確に言語化されていないだけで直積と部分集合という抽象的な概念は既に頭の中にあるわけです。
例えば「比例」って概念は中学校で習いますが、別に難しくはありませんでしたよね。
それは僕らが日常生活で無自覚に「比例」という概念を形成しているからです。
歩行する速度に対して目に映る景色の変化こそ「比例」です。
x軸方向が歩く速度、y軸方向に見える物体の大きさ。
xに比例してyは大きくなります。
実は普通に生きているだけで比例の概念を僕たちは獲得しているわけです。
義務教育程度の数学は潜在意識の知識を意識レベルへ引き上げる作業だと言えますよね。
人はそれを自覚していなかったり、その使い方を知らないだけで誰でも優れた能力を持っていると僕は信じています。
だからこそ、僕はボクシングの習得において一般論で言われている「意識→無意識」の真逆の論理である、「無意識→意識」を強く主張しています。
今回は「関係」について。
僕らはこれを無自覚に定義しています。
どんな風に僕らが「親子」「恋人」という関係性を定義しているのか気になりませんか。
関係
まずは直積の概念から。
直積
直積の定義に関しては上に貼った記事を参照してほしいのですが、簡単に復習すると
具体的に二つの集合 A, B に対し、それらの直積とはそれらの任意の元 a ∈ A, b ∈ B の順序対 (a, b) 全てからなる集合をいう[1]。
Wikipedia
$A × B = \{(a,b)|a \in A \land b \in B\}$
そんなに難しくはありません。シンプル。
$\A land B$は論理積の記号です。
もう少しイメージしやすくすると以下。

このように集合A,Bの順序対の組み合わせを集めたものを直積集合と呼びます。

もっと身近なものだとxy座標です。
$\mathbb R × \mathbb R$
左図が実数の直積集合を視覚化しているものだと分かると思います。
順序対なので(2,1)と(1,2)が異なります。
順序対の定義なども上の記事にありますので、参照してください。
xy座標を習った時に難しさは感じませんでしたよね。
恐らく僕達が無自覚に直積を定義していたからです。
直積集合の復習を終わります。
次に部分集合
部分集合
細かい部分集合の定義は集合論の流れでやりたいので、ここでは細かくやりません。
一応定義を載せておくと
集合 A の要素はすべて集合 B の要素でもあるとき、すなわち、
Wikipedia
$\{ \forall x(x\in A\rightarrow x\in B)\}$
が成り立つとき、A は B の部分集合であるといい、
$A \subseteq B$
で表す。
翻訳すると集合Aの元xが集合Bに含まれているのなら、集合Aは集合Bの部分集合となります。
ここでは深掘りしませんがAとBが同じ場合も部分集合に分類されます。
AとBが等しくない場合は真部分集合と呼ばれます。
「関係」に話を戻します。
関係
関係の定義が直積集合の部分集合であることを簡単に例を挙げて説明します。
父親を集めた集合Pと子供を集めた集合Cを用意します。
$P × C = \{(x,y)|x \in P \land y \in C \}$
直積集合P × Cは父親という属性と子供という属性を持っていれば誰でも組み合わせられるので、親子でない組み合わせもあります。
関係を示すためにさらに部分集合Rを定義します。
$R = \{(x,y) \in P × C | xとyが親子\}$
このように定義した場合に直積集合 P × C から親子関係のある集合Pを抜き出せて、これは「関係している」とできます。
「関係」というありふれた言葉を数学ではこのように定義して考えます。
些細でつまらないことのようですが、「言葉を定義する」ことは議論を進めるためにとても大切なことですよね。


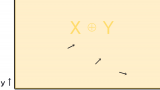
コメント
{ 「関係」というありふれた言葉 }を、数の言葉について[ 【1】の存在量化(∃) ]の記事を見つける。
・・・ ・・・
≪…思考や理性の法が愛にしたがっているのだ。
愛を手に入れるには、まず愛が感情ではなく、存在であるということを知ることだ。…≫を、
「アミが来た」エンリケ・バリオス著 絵・訳 さくらももこ+うんのさしみ の
「わたし、世界は愛によって結ばれるべきだって、本に書いてみたいな」
とペルリータ(真珠)はいった。
とある。
これを、
[ 【1】、数はi(アイ・虚数)によって結ばれるべきだって、本に書いてみたいな]
と[私の情念]はいった。
としたい。
絵本の力で、数の言葉ヒフミヨ(1234)が平面(2次元)からの送りモノとして眺めると、〇 △ ▢ に、水滴(露)・(涙) 猫のコトバ 猫のしっぽ などに想いをめぐらす。
岡潔の数学体験館が来春できるとか、それに関係して【1】を問う森田真生著の絵本「アリになった数学者」や松谷みよ子「あかちゃんのわらべうた さよならさんかくまたきてしかく」 長谷川義史訳「サンカクさん」 などから 数学の根源たる【1】をカタチ(〇△□ながしかく)と相対的な視座で・・・
・・・ ・・・
就活の女のスーツらいてい忌 (香苗)
から、
らいてい忌ヒフミヨこれぞ太陽だ
のじゅじゅつなぎ 句 を、
「松谷みよ子 あかちゃんのわらべうた
さよならさんかくまたきてしかく
上野紀子 え」
に、数学文化からの
カタチ(〇△□ながしかく)
言葉の点線面
演算符号(+-×÷√=)
十進法の基における西洋数学の成果の符号(i e π)
無限(∞)
数字([1][0])
文脈命題の符号(∃ ∀)
数式 方程式
直交座標 極座標 など と
桁表示の数字(2 3 4 5 6 7 8 9)
をウマク纏め上げているのを数の言葉ヒフミヨが、平面(2次元)からの送りモノとして眺めると、興味深い・・・
さよならさんかく
またきてしかく しかくはおふとん
[さんかくはしかくになってさようなら]
( √さんかく(斜辺(√n)) ⇒
『ヒフミヨ矩形』 )
おふとんは ねんね ねんえは ねこ
[ ねんね根ヒフミヨしかく√(ルート)さん ]
( ねんね根1を割っては√2と )
ねこは あるく しっぽを たてて
[ ねんね根ヒフミヨ進i(アイ)たてて ]
( 『自然比矩形』 ⇒ 正方形(1×1))
あるくは おつきさま ねこが あるけば いっしょに あるく
[ ヒフミヨはまんまるさまだπに生る ]
( i(アイ)たて(□) ⇒
ヒフミヨ(〇) )
おつきさまは まるい
まるくて ひかる あいつは なんだ
[ まるいπひかるあいつは中心だ ]
( 〇(π(2π)) ⇒
中心(0・原点) )
ひとつめこぞう! こぞうは おばけ
[ まるいのはぐるぐるちゃんおばけだよ]
( 極座標 ⇒ 原点 )
おばけは ぞろぞろ ふらふら ゆれて
ひゆー どろどろどろ
おばけは・・・・・・きえる
こんにちは こんにちは
こんにちは こんにちは
[ おばけとはπに連れ添うi(アイ)とe(イー) ]
( i(アイ)たて(□) ⇒
極座標(オイラーの等式) )
ぺかっと きえた きえるの なあに
でんきが きえた おやすみなさい
おやすみなさい おやすみなさい
[ ぺかっときえるのなあにかでんきだよ]
( 光(電気)が潜む ⇒
実数直線(あした(時間軸) )
みんな ねんね
おやすみなさい
[ ヒフミヨはおやすみなさいあしたくる]
( カタチ(〇△□ながしかく)の送りモノ
⇒ ひ・ふ・み・よ・い・
む・な・や・こ・と )
自然数の[1]は、まんまるさまの送りモノとして眺めると、
文化の日1の始まり〇に棲む
絵本「すうがくでせかいをみるの」で、[1]を単位化(割るという意味)を、平面(2次元)からの送りモノとして眺めると、
シカクさん(コスモス)を基にすると、
1/√2 が、[1]だ。
(1/√2)²×(1/√2)²=(1/2)+(1/2)
=1=(√1)²=1
□の、[1]は二次元の 1(1×1)
まんまるさん(カオス)を基にすると、
1/√π とすると、
円周は、[2√π]( 2π(1/√π) )に、
円の面積は、[1]( π(1/√π)² )に、
これを、円を描く(1周する)行為が、[ さよならさんかくまたきてあした ]で、4次元を獲得し、幽霊(カオス)な□(√π×√π)が、数直線上の2を刻む、√πを極座標ではπ(180°)回転の操作、直交座標ではπ/2(90°)回転の操作として、それぞれ円環上か直線上を数の言葉ヒフミヨが進んでいると観える・・・
[人]は、1・2・3・4次元で閉じ(計算でき)ている数の言葉を「さよならさんかくまたきてしかく」に眠り(無意識)で見つけたようだ・・・
おばけは、[ひ・ふ・み・よ・い・む・な・や・こ・と]の10までの刀模様の物差しに生る。(『幻のマスキングテープ』)
・・・ ・・・
との記事を見つける。
サンカクさんでの【1】の想いは、
大きな△の辺は、半径1の円環の3等分の弦(辺(√3))で、(2π/3)の3歩(回り)で頂点が円環で共有できる。
中くらいの△の辺1は、半径1の円環の6等分の弦(辺(1))で、(2π/6)の6歩(回り)で頂点が共有でき辺(1)で円環と中心を繋いでいる。
小さい△を、
≪…愛とは意識の繊細(デリケート)な一成分のことである。
それは存在の深い意味を教えてくれる。…≫で、
大きな△の辺を、√3で単位化(割るというコトは、【1】をつくるコト)すると、(1/√3)である。
大きな△の2辺が、時間軸とする実数直線とするのを、△さんの2次元(平面)としての【1】は、3の
(-1/2)乗根の(-1/2)乗根で、3の(-/4)乗根の2たつ(辺)が、時間(4次元)を刻んでいると観える
( 辺(2×(3の(-/4)乗根))の△の広さは、1=1×1 ) ・・・
実数直線には、1・2・3・4次元が棲めるのが、「さよならさんかくまたきてしかく」から[さよならさんかくまたきてあした]と・・・
△さんよありがとう・・・
夏目漱石著「草枕」三の
[□ ⇒ △]の文脈に辿り着く・・・
πと1〇と□のなぞり逢