今回は極限に挑戦します。
高校でやったので曖昧には知っていましたが、本来の厳密な定義は一筋縄ではいかず苦労しました。イメージ自体は難しくないんですが数学独特の表現が難しい。
それでは学んだことをアウトプットしていきます。
ところで、何故『極限』を学ぼうと思ったのかを先に説明します。
極限を知って微積分を理解する
そもそも数学を学ぼうとした発端は、ボクシングを理解するために力学を深く理解したいと思ったからで、そのためには微積分学を学ぶ必要があるからで、微積分学を理解するために基本的な数学の知識が必要だと感じたからです。
力学は基本的に微積分で記述します。そして、微積分には極限という概念の理解が不可欠です。
根本を理解できないと、話が進む内に理解が曖昧になって最後にはバラバラに砕けてしまうのは高校で経験しましたので、定義からいきます。
数列の極限
高校で極限は「限りなく近づく」って曖昧な表現で教えられましたが、厳密さを求める本来の数学では「限りなく」とか「近づく」という曖昧な言葉の意味を、数学的な記法で厳密に定義しなければなりません。
厳密に「限りなく近づく」を数学で表現する方法が以下のε – N論法です。
本当は「数列」の定義からやらなきゃなんですが、面倒なので今回は飛ばします。
数が並んだやつです。
ε-N論法
$\displaystyle\lim_{n \to ∞}\mathrm{a}_n = α$
極限はこんな風に記述します。
「数列$a_n$を限りなく大きくするとαに収束する」という意味です。
イメージはできますよね。
それでは定義を確認していきます。
数列$a_n$の極限がαに収束するとは
どんなε(イプシロン)にも対応する数列$N \in \mathbb{N}$が存在し適切なNを取れば、n > Nなら$\vert \mathrm{a}_n – α \vert < ε$になること。
これでも僕が分かりやすく翻訳してますからね。日常でもしこんな話し方する奴がいたらとりあえず一旦シバきます。
翻訳するまえの数学の表現はもっともっと分かりにくくて地獄です。

これがε – N論法による極限の定義です。
マジです。
もう少し分かりやすく翻訳してみると、
「任意のεに対応するNがあって、適切にそのNを設定し、そのNより大きい範囲nにおいて$\vert \mathrm{a}_n – α \vert < ε$の条件を満たすなら、数列$a_n$の極限が存在していると言っていいよ」
です。
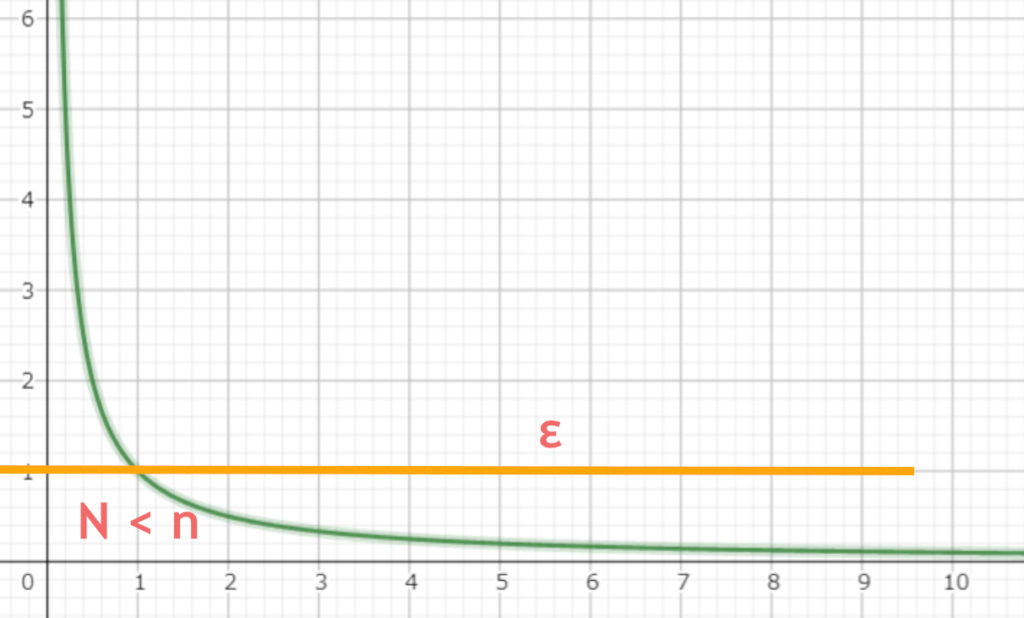
ε = 1でとってもそれより小さな$\vert \frac{1}{x} – 0 \vert$を成立させるnが続いています。
εをどれだけ小さくしていってもNをそれに応じて大きくしていけば$\vert \frac{1}{x} – 0 \vert$ < εが成立します。
イメージとしては「ある数列を無限に大きくしていくと、ある一点に向かっていく」ってだけです。
「限りなく近づく」ってイメージは間違ってないんです。
ただ、数学は曖昧さを許さない。
人間のイメージが追いつかなくなることもあります。
簡単な数列ならなんとなくイメージできますが、数列の形が複雑になればなるほど、どこに収束するのかってイメージが湧きにくくなります。
厳密に「限りなく近づく」ための手順を用意しておけば、その通り手順を踏むだけで複雑な数列の極限をとることができます。
簡単に実例をε – N論法を見てみます。
実例1
先ほどのグラフの例をε – N論法で証明してみます。

$\frac{1}{n}$の数列のグラフです。
$\frac{1}{n}$が0に収束するためには、$\vert \mathrm{a}_n – 0 \vert < ε$となる、εに対応するn > Nが存在する必要があります。
任意のεを試しに1にします。
0は引いても何もしないので消します。
$\vert \mathrm{a}_n \vert < 1$
こんな式になりますね。
数列$\vert \mathrm{a}_n \vert$は$\frac{1}{n}$なので
$\frac{1}{n} < 1$
この不等式が成立するn > N、つまりあるNから先のすべてのnで上の不等式が満たせればいいんです。
Nに1を与えた場合、それより大きな2が自動的にnに与えられます。
$\frac{1}{2} < 1$
条件を満たします。
そしてn > 1の場合すべてのnが「1より小さい」という条件を満たします。
このεは任意の正の実数なので極端に小さな数でも指定できます。
0.00001と置いてみます。
この場合もNを100000と置けば自動的にnはNより大きな数になるので
$\frac{1}{100001} < 0.00001$
ほんの少しεより小さくなりました。
これをいくら繰り替えして、εをどれだけ小さくしてもNを大きくして対応していけばいいだけなので、
$\vert \mathrm{a}_n – 0 \vert < ε$
は成り立ちます。
つまり定義の条件を満たすので、$\frac{1}{x} < 1$の極限は0に収束すると証明できました。
別の例を挙げます。
実例2

青はy=1の直線です。
緑の曲線は$\frac {n+2}{n+1}$です。
nを大きくしていった時の極限は1に収束します。
緑の曲線が青のy = 1直線に収束していくのが分かりますね。
この式を極限の定義に従って、極限があることを証明していきます。
先ほどのようにεを1とします。
極限は1に近づいていくので、目標となる値は1、αに1を代入します。
$\vert\frac {n+2}{n+1} – 1\vert < 1$
分かりやすく式を変形して
$\vert\frac {n+2}{n+1} – \frac {n+1}{n+1} \vert < 1$
$\frac {n+1}{n+1}$は約分すると1ですね。
強引に計算可能な形に式を変形します。
$\vert\frac {1}{n+1} \vert < ε$
分子のnが消えました。
εに何を設定したとしてもこの条件を満たすNが存在し、かつそのNの先の数列n達に対しても当てはめることを証明できればいいんです。
$\vert\frac {1}{n+1} \vert$がε = 1より小さくなるのはn ≧ 1。
Nを0とすることでn > Nは全てεより小さくなり、条件を満たします。
εを0.00001とと小さくしても同じです。
Nを100000とすればεをほんの少し下回ります。
εをどれだけ小さくしていってもNを∞に大きくすることで、ε – N論法の条件を満たします。
$\frac {n+2}{n+1}$には極限が存在し、その極限値は1となります。
ここまでくるとイメージできたと思いますが、数列と極限値の差がどこまでも小さくできた場合、その数列の極限を定義することができるってことです。
$\vert\frac {1}{n+1} \vert$は$\frac {n+2}{n+1}$の極限値1と1の差のことです。
この差がどこまでも小さく(任意のεと同義)していける場合、極限を定義してもいいとε – N論法は説明しています。
極限なし
極限がある場合を考えたら極限がない場合も考えたくなるのが人情。
$\displaystyle\lim_{n \to ∞}(-1)^n$
この数列は値がとびとびになるのは何となく予想できます。
この数列のnの値を3,4,5とどこまで大きくしていっても$(-1)^n$の数列は奇数の場合にマイナス、偶数の場合にプラスとなり、とびとびの数列になります。
任意のεに対してどんなNをとっても滑らかな数列は存在しません。
つまりこの数列に極限は存在しないと言えます。
発散
以上は収束する場合の値でした。
今度は発散する場合を考えます。発散は∞にどこまでも数が大きくなる数列です。
簡単にこんな式で考えます。
$\displaystyle\lim_{n \to ∞} a^n = ∞$
ある数を∞乗したら無限に大きくなるよねってだけですが、まずは定義通り確認します。
例えば分かりやすく$2^n$で考えます。
ε = 1000をとって、その値を超えるn > N を考えます。
2を10乗すれば1024になるので、εを超えます。
εをどれだけ大きくしてもNの値を大きくすることでn > Nなら$\vert \mathrm{a}_n \vert > ε$という条件を常に満たすことができます。
よって$2^n$は極限の定義に当てはまります。
ここまでが数列の極限の定義です。
簡単に復習すると。
どのεにも対応する数列$N \in \mathbb{N}$が存在し、適切なNを取れば、n > Nなら$\vert \mathrm{a}_n \vert > ε$が真になる場合、極限が存在する。
簡単に表現すると、$\vert \mathrm{a}_n \vert < ε$の差が極小になっても滑らかな数列が続いていることを証明すればいいのです。
それを厳密に定義しようとするとε – N論法のような複雑な言い回しになってしまいます。
ほんとに曲者でした。ε – N論法。
数学語に慣れていないというのが最大の障壁で、外国語みたいで頭に少しも入ってきません。
でも今回、数学語がほんの少し理解できるようになりました。
この調子で続けていけば言語みたいにすらすら頭に入ってくるんじゃないかと思います。
やる気がでてきました。
次は極限の性質について学びます。



コメント