黄金比

黄金比（おうごんひ、英: golden ratio）とは、次の値で表される比のことである：

$\displaystyle 1:{\frac {1+{\sqrt {5}}}{2}}\,.$

黄金比における

$\displaystyle {\frac {1+{\sqrt {5}}}{2}}$

を黄金数（おうごんすう、英: golden number）という。

ウィキペディア

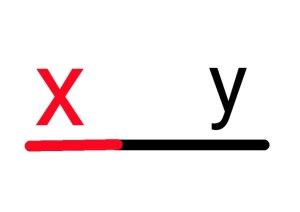
x:y=y:y+x

x:y=y:y+x
となるような直線があると仮定します。

a:b=b:a+b(比例式)
b²=a(a+b)(比例式法則)…※1
b²=a²+ab(分配法則)
b=√a²+√ab(指数法則)
b=a+√ab(べき乗)…①

a=1と仮定した時のbとの比を求めます。
①へ仮定を代入。
b=1+1･√b(①)
b=1+√b(乗法単位元)…②

√b=xと仮定して②へ代入
x²=1+x(①)
x²-x-1=0(加法逆元)…※1

この解は既述した再帰的な比を構成します。

べき乗の分配法則　$a^{xy}=(a^{x})^{y}$

べき乗実数 x の正整数 n 乗は、素朴には、n 個の x を掛け合わせたものである。厳密には、次のように再帰的に定められる。 (∗)x¹:=x,(∗∗)xn+1:=xⁿ×x(n≥1).x0 を定義する場合には、関係式 (∗∗) が n ...

平方完成

今後の為に二次方程式ax²+bx+cの解を求める法則を導いておきます。

以前導いた展開法則を用います。
$(x+y)²=x²+2xy+y²$(展開法則)※2

$ax²+bx+c$(仮定)
$a(x²+\dfrac{bx}{a})+c$(分配法則)
$a(x²+\dfrac{bx}{a})+\dfrac{ab²}{4a²}-\dfrac{ab²}{4a²}+c$(加法逆元)
$a(x²+\dfrac{bx}{a}+\dfrac{b²}{4a²})-\dfrac{ab²}{4a²}+c$(分配法則)
$a(x+\dfrac{b}{2a})²-\dfrac{ab²}{4a²}+c$(※2)
$a(x+\dfrac{b}{2a})²-\dfrac{b²}{4a}+c$(乗法逆元)
$ax²+bx+c→a(x+\dfrac{b}{2a})²-\dfrac{b²}{4a}+c$(→導入)…※2

黄金比

以下は黄金比の導出。

※2を※3で変形。

$x²-x-1=0$(※2)
$(x-\dfrac{1}{2})²-\dfrac{1}{4}-1=0$(※3)
$(x-\dfrac{1}{2})²-(\dfrac{1}{4}+1)=0$(分配法則)
$(x-\dfrac{1}{2})²=\dfrac{1}{4}+1$(加法逆元)
$(x-\dfrac{1}{2})²=\dfrac{5}{4}$(分数加法)
$x-\dfrac{1}{2}=\pm\sqrt{\dfrac{5}{4}}$(指数法則)
$x-\dfrac{1}{2}=\dfrac{\pm\sqrt{5}}{2}$(指数法則)
$x=\dfrac{\pm\sqrt{5}}{2}+\dfrac{1}{2}$(加法逆元)
$x=\dfrac{\pm\sqrt{5}+1}{2}$(分数加法)

黄金数$x=\dfrac{\pm\sqrt{5}+1}{2}$が導出できました。

黄金比は
$1:\dfrac{\sqrt{5}+1}{2}$
※比なのでマイナスはない。

無理数が自己増殖構造なの面白い。