行列と複素数って、回転だって直感を覚える。この二つはなんとなく似てね？って。
虚数は実数とは異なる次元がある。二つで一つ。
二つの情報の摩擦がそれらと異なる意味の方向に現れることを表現したり。例えばx軸上の二つの物体の衝突が回転って軸に飛び出したり。
ヒトの目には二つに見える情報でも、物理的には一つの情報で構成されていたり。例えば、光の強さって一つの情報が、床の影の形や濃さって二つの異なる要素(≒次元)で構成されてる、みたいな。
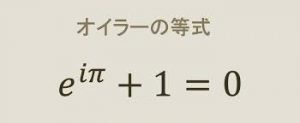
ひとまずはこんな理解。ヒトの認識空間では二つの要素で構成されているんだけど、物理的にはそれらは同一。同じ物体の別の側面。
仮にそうだとするなら、二行二列も複素数に見えね？と。
その直感をaiと議論。今回はその結果のお話。
二行二列の行列と複素数は同値と仮定。$x=f(a+bi)=\begin{pmatrix}a&-b \\b & a\end{pmatrix}$(仮定①)
都合のよく具象化。
この仮定が複素数が満たしていてほしい性質を満たすことを示す。
上の仮定①の加法の相手方を仮定。
$y=f(c+di)=\begin{pmatrix}c&-d \\d & c\end{pmatrix}$(仮定)
行列の加法はWIISを参照。同じ大きさの行列の同じ成分を足すだけ。
複素数を仮定①により変形し行列加法をするのと、そのまま複素数として普通に加法した結果が論理的に同値であることを証明したい。
複素数空間と行列空間の+×の挙動が同じなら、それらはそれらを見る為の形式化ってメガネが異なるだけの同じ空間だよねって。
すなわち、
$f(x+y)=f(x)+f(y)(仮定②)$
であることを証明したい。つまり、複素数空間と行列空間の加法が同じ規則であることを示したい。
雑に言い換えると、文脈を固定するなら、日本人の「おお！」とアメリカ人の”WOW！”は形が異なる同じ意味として理解でにるよね？たいな。
日本語と英語は形式が異なるだけで、ヒトの心や認識を表しているよね。完璧な一対一対応が作れたら、それらは同じものどよね、ってこと。
その為には上の仮定①が成立せすなら②が成立することを示せば良い。
加法
まずは複素数の加法
$(a+c)+i(b+d)$(複素数加法と分配法則)
単純に実部と虚部を出すだけ。規則性が行列と似てるよね。
そして結果をf()で行列空間へ送る。
結果は
$f((a+c)+i(b+d))=\begin{pmatrix}(a+c)&-(b+d)\\(b+d)&(a+c)\end{pmatrix}$(仮定①より)…#1
次は別々に行列空間へ送ってから足してみる。
$f(a+ib)+f(c+id)$(仮定)
$\begin{pmatrix}a&-b\\b&a\end{pmatrix}+\begin{pmatrix}c&-d\\d&c\end{pmatrix}$(仮定①)
$\begin{pmatrix}(a+c)&-(b+d)\\(b+d) &(a+c)\end{pmatrix}$(行列加法)
#1と同値
すなわち複素数を①のような行列と仮定すると複素数の加法が常に成立する。
次は乗法。
乗法
$(a+bi)(c+di)$(複素数)
$ac+adi+cbi+bdi^{2}$(乗法展開)
$ac+adi+cbi-bd$(虚数の二乗)
$(ac+bd)+i(ad+bc)$(交換法則と分配法則)…#2
複素数の乗法
行列の乗法は列と行の要素をかける。この意味を今考えると先に進まないので、それは次回に譲り式の展開を続行。
次は複素数を行列に変形し、行列の乗法。
$\begin{pmatrix}a&-b\\b&a\end{pmatrix}\begin{pmatrix}c&-d\\c&d\end{pmatrix}$(①より)
$\begin{pmatrix}(ac-bd)&-(ad+bc)\\(ad+bc)&(ac-bd)\end{pmatrix}$(行列乗法)
$(ac+bd)+i(ad+bc)$(①より)
#2と一致。
仮定した複素数と行列の関係を基にそれぞれの乗法法則を保存したまま同じ結果が導かれました。すなわち両者は同じ構造。
WOW！=おお！
よって
虚数は
$i=0+1i=\begin{pmatrix}(a+c)&-(b+d)\\(b+d)&(a+c)\end{pmatrix}$
立体的な数を平面で解釈して辻褄を合わせると虚数って奇妙なな数が必要になったってことかなと。
ある次元の衝突が別の次元に飛び出すって普遍的に起こりますよね。根にあるのはこの普遍的な考え。二つの次元の作用が別の次元の意味を創り出すって規則は物理的にも都合が良いことが多い。
量子などの物質に応用すると奇妙な解釈が生まれてしまう。
コメント