公理主義実数論
集合 G とその上の二項演算 μ: G × G → G の組 (G, μ) が群であるとは、以下の3つの条件を満たすことをいう:
(結合法則)任意の G の元 g, h, k に対して、μ(g, μ(h, k)) = μ(μ(g, h), k) を満たす:
(∀g,h,k∈G)[μ(g,μ(h,k))=μ(μ(g,h),k)].(単位元の存在)μ(g, e) = μ(e, g) = g を G のどんな元 g に対しても満たすような G の元 e が存在する:
(∃e∈G)(∀g∈G)[μ(g,e)=μ(e,g)=g].このような e は存在すれば一意であり、G の単位元という。
(逆元の存在)
G のどんな元 g に対しても、μ(g, x) = μ(x, g) = e となるような G の元 x が存在する:
(∀g∈G)(∃x∈G)[μ(g,x)=μ(x,g)=e].このような x は存在すれば一意であり、この x を g の G における逆元といい、しばしば g−1, あるいは演算を加法的に書く場合には −g で表される。
G に二項演算(”*” と書くことにする)が定義されていて、以下の条件
結合法則:
a∗(b∗c)=(a∗b)∗c
単位元の存在:
∃1; a∗1=1∗a=a
逆元の存在:
∀a,∃a⁻¹; a∗a⁻¹=a⁻¹∗a=1
交換法則:
a∗b=b∗a
(ただし、a, b, c は G の任意の元)を全て満たすとき、G と演算 “*” の組 (G, *) をアーベル群という。考えている演算があきらかなときは省略して単に G をアーベル群と呼ぶ。
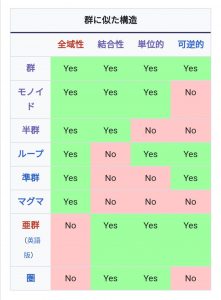
群は、1.集合とその中の閉じた演算、2.結合法則、3.単位元、4.逆元、が定義できる対象。さらにそれに交換法則を加えたのが可換群(アーベル群)。
自然数加法と乗法は逆元がないので群ではありません。モノイド。
整数の加法は閉じた演算、かつ作用させても要素を変化させない単位元0と、作用させると単位元になる逆元が定義できます。よって群。交換法則も成り立つので可換群。
整数の乗法は作用させても変化を起こさない単位元1が定義できますが、逆元はありません。
例えば整数には、2nを単位元1へ送る乗法の要素がありません。よってモノイド。
有理数の加法と乗法は群、かつ可換群。
関数を要素、その合成を演算とした場合は非可換な群。
その心は
以下は長濱説。
演算は関係。1+2=3は関係。
ヒトは、認識可能なある対象と、それとは別の対象の連続的な接続の間に「関係」として意味を見いだす。親子、夫婦、過去今現在、順序、必要十分条件、同一視など。
ヒトが意味を感じられる「関係」の規則性を抽出する。
1結合法則
ヒトの認識においては、対象の接続の順序を変えただけでは、その意味は変化しない。故に結合する順序でその意味が変化されるのは困る。
(((私は)長濱陸)です)
(私は(長濱陸(です)))
これで文の意味が変わらないことの要請。
あるいは
過去(今(未来))⇔((過去)今)未来
この関係が常に保持さるのことの要請。
また、右から見て左から見て、その見え方が変化したとしても、構造そのものは変化してほしくない。それが交換法則(可換群)。
親→子、親←子
二つの順序を入れ替えた場合に、その関係の意味が「親子」から「恋人」に変化するのは困る。ヒトの認識では理解ができない。
もしかしたら見る角度によって現実は変わるのかもしれないが、だとしても、それはヒトの理解を超えているから、ひとまずは無視する。現実とは無関係にされている要請。ある意味では願い。
認識規則を厳密化しておくと、未知の構造に遭遇しだ時に、それにどんな性質があるのかを帰納的か演繹的に導くことができるから効率が良い。記号化された形式的な処理を現実の動きに見立てて、その微細な変化を追跡できる。
物理空間の近似をコンピューター上に作り上げれば、あらゆる実験を一瞬で完結させられる。また何万回も実験できる。コストも比較的にかからない。
群やモノイドなどの既知の空間を定義しておくと、そうでない未知の空間が現れた時に対処がしやすい。未知の空間と既知の空間の関係を比較し、その性質を明らかにできる。
自然数を足場に負数、整数、有理数、無理数、虚数が導かれたようなこと。
厳密に分解、分類しておくことで、既知の空間と未知の空間の判別が迅速になる。
現実がそうなっているのかとは無関係な願い。



コメント