対偶

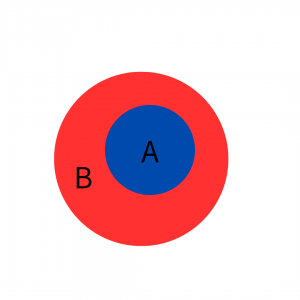
A={(x,y)∈ℝ²|y³+yx²≤x³+xy²}
B={(x,y)∈ℝ²|y≤x}

⊂集合を論理の包含関係→⇒と解釈します。

y³+yx²≤x³+xy²(仮定)
y(y²+x²)≤x(x²+y²)(分配法則)
y(x²+y²)≤x(x²+y²)(交換法則)
ya≤xa(代入)
y≤x(乗法定義)
y³+yx²≤x³+xy²→y≤x(→導入)
y³+yx²≤x³+xy²⊂y≤x(⊂定義)
A⊂B(代入)

xとyへ同じ値を乗じた場合の大小関係から、y≤xが成立することが導出されます。

自然数の冪集合は自然数全体を部分集合として含みます。

⊂と⇒は下の包含関係を表す別の記号なので、論理的には同値関係と仮定します。①

また、∨と∪も論理的に同じ操作だと仮定します。②

A=2^n
B=ℕ

B⊂A(仮定)
B⇒A(①)
A∨B(仮定2)
A∨A(⇒推移律)
A(べき等律)
(B⊂A)∧(A∪B)→A(→導入)③

自然数の集合族の和集合が自然数であることが証明できました。

冪集合（べきしゅうごう、英: power set）とは、数学において、与えられた集合から、その部分集合の全体として新たに作り出される集合のことである。

ウィキペディア

引用ワイズ

集合の濃度

有限の濃度の推移律

|A|=|B|∧|B|=|C|⇒|A|=|C|
濃度に推移律が成り立つことに証明。

〜は一対一対応関係。

A〜B,A⊆B,B〜C,B⊆C(仮定)
A〜B∧B〜C(∧導入)
A〜C(推移律)
A⊆B∧B⊆C(∧導入)
A⊆C(⊆推移律)
A〜C∧A⊆C(∧導入)
|A|≤|C|(濃度定義)

自然数と偶数の濃度の同値関係

自然数と偶数の要素の数が可付番であること、すなわち濃度が同等(全単射性)であることの証明。

偶数を任意の自然数の二倍2aと定義します。

∃y,∀x∈ℕ(2x=y)

これは証明するまでもなく自然数の定義より明らか。
自然数の乗法は閉じており、任意の自然数は二倍しても自然数です。
つまり、自然数(可算集合)と偶数は全単射性がある可算集合。すなわち濃度は同じ。

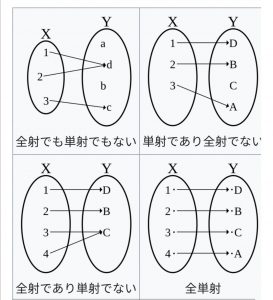
全単射
集合 $X$ と $Y$ の間に全単射が存在するとき $X \approx Y$ と書き、 $X$ と $Y$ は濃度が等しいという。集合 $X$ から集合 $Y$ のへの単射が存在するとき $X ≾ Y$ と書き、 $X$ の濃度は $Y$ の濃度以下であるという。集合 $X$ と $Y$ について、 $X ≾ Y$ だが $X \approx Y$ でないとき、 $X ≺ Y$ と書き、 $X$ の濃度は $Y$ の濃度より小さいという。

ウィキペディア

可算集合（かさんしゅうごう、英語: countable set または denumerable set）または可付番集合とは、おおまかには、自然数全体と同じ程度多くの元を持つ集合のことである。各々の元に 1, 2, 3, … と番号を付けることのできる、すなわち元を全て数え上げることのできる無限集合と表現してもよい[1]。

ウィキペディア