我流で負数の定義を考え続けると熱が出そうなので、素朴集合論で息抜きします。
Aの部分集合Bとその差集合を考えます。
人の認識を土台として図式化するならこう。
これを定義します。
Aという集合からBという集合を引く演算があってほしいですよね。
日常な動物という集合から犬という集合だけを引いて、残りの動物について考えたい、みたいな心の働きを定義したのが集合の減法や補集合、差集合の認識。
差集合(さしゅうごう、英: set difference)とは、ある集合の中から別の集合に属する要素を取り去って得られる集合のことである[1]。特に、全体集合 U を固定して、U からその部分集合 A の要素を取り去って得られる集合を A の補集合という[2]。
Wikipedia

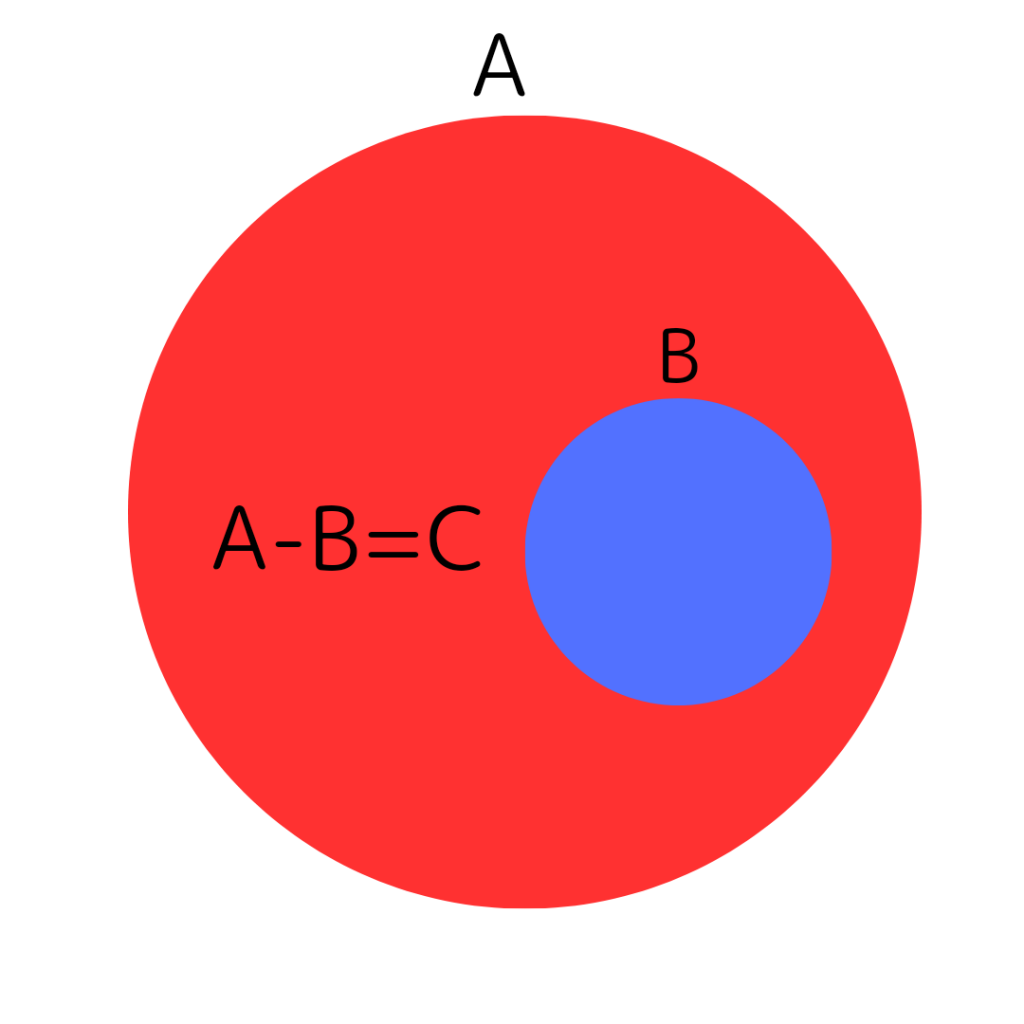
集合Aから集合Bを引いたのが集合Cであってほしいですよね。そうだなければ人の認識と整合しません。その願いを元にすると、参考書のような定義が自動的に浮かび上がります。集合Aとその部分集合Bがあって、※部分集合に関しては雰囲気で1.x∈A→x∈B∨x∈(A-B=C)2.x∈B→x∉(A-B=C)3.x∈(A-B=C)→x∉B全体の印象としてはC=A-CB=A-CA=B+Cを定義しているのじゃないかなと。こう定義することで自動的に導かれる集合の性質(定理)を考えます。A⊂Bと花庭するとA-B=CA-C=BB+C=A(1を加法として解釈)集合Aから集合Bを引いたのが集合Cであってほしいですよね。そうだなければ人の認識と整合しません。その願いを元にすると、参考書のような定義が自動的に浮かび上がります。集合Aとその部分集合Bがあって、※部分集合に関しては雰囲気で
1.x∈A→x∈B∨x∈(A-B=C)
2.x∈B→x∉(A-B=C)
3.x∈(A-B=C)→x∉B
全体の印象としてはC=A-CB=A-CA=B+Cを定義しているのじゃないかなと。こう定義することで自動的に導かれる集合の性質(定理)を考えます。A⊂Bと仮定すると
A-B=C
A-C=B
B+C=A
もっと厳密化できん?演算を。という気がするのですが、まあでもこんなものかなあと。
引用:


コメント