論理包含の演算規則はは認識を一般化したものだと仮定して、もう少し論理包含について認識の側面から考えます。
論理包含の定義から同値という概念を演繹出来ます。僕がずっと抱いている「なぜ同値の定義の形はそうなっているのか」という疑問の答えへ繋がっていました。
論理包含から同値
まずは必要条件、十分条件、必要十分条件について。
必要条件や十分条件という言葉は日常で使われると思いますが。使われるとめっちゃ混乱しますよね。「えっと…どれがどれだたけ…」って。
恒真式
必要条件、十分条件を知る前に恒真式の定義を知る必要があります。
【トートロジー(恒真式)】
$P\to P$「前件と後件が真」か「前件が偽」の時に真となる、つまり同語反復の場合はPの真理値の如何に関わらず含意は常に真となります。
Wikipedia
恒真式は恒(つね)に真となる論理演算のことです。
人の認識の延長線上で説明するなら、「如何なる解釈においても変化しない認識」のことだろうと思います。
「私は私だ」とか「失敗するか成功するかのいずれかだ」とか。
論理式にすると
a→a
「aならばa」
aの真偽は問わず上記の含意の演算結果は真となります。
a∨¬a
「aかaではない」
論理和と否定を使った演算。論理和はいずれかが真ならば真となるので、aの真偽を問わず恒に真となる演算です。
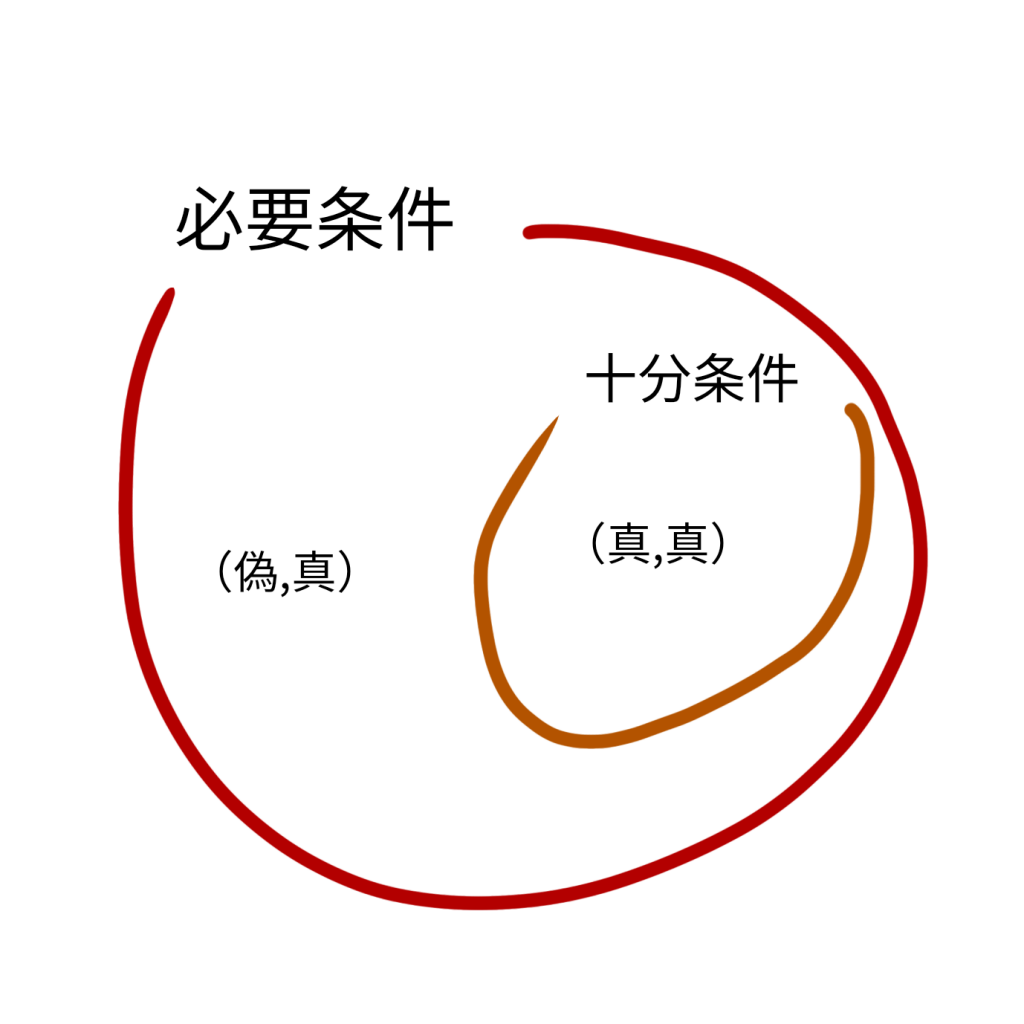
必要条件と十分条件の定義
二つの条件 p 、q に対して、「 p を満たすものは全て q も満たす 」 というとき、「 p は q である為の十分条件である 」 あるいは 「 q は p である為の必要条件である 」 という。
また、「 p は q である為の十分条件であり、q は p である為の十分条件である 」 というとき、「 p は q である為の必要十分条件である 」 あるいは 「 p と q とは同値である 」 という。
Wikipedia
含意の結果が恒に真となる恒真式である場合のみ
p→q
前件pは後件qの十分条件
後件qは前件pの必要条件
となります。
具体例で考えると。
$x=2 \to x^2=4$
は恒真式です。
すなわち、$x=2$は$x^2=4$は十分条件、$x^2=4$は$x=2$の必要条件となります。
また「等しい(同値)」とは論理的な必要十分条件のことだと定義されています。
pがqの十分条件を満たし、qがpの十分条件を満たす場合を同値と定義するわけです。
同値類の定義の文脈が浮かび上がってきました。
【同値類の記法と定義】
同値関係は二項関係 ∼ であって以下の3つの性質を満たすものである[4]:
X の任意の元 a に対して,a ∼ a である(反射性),
Wikipedia
X の任意の2元 a, b に対して,a ∼ b ならば b ∼ a である(対称性),
X の任意の3つの元 a, b, c に対して,a ∼ b かつ b ∼ c ならば a ∼ c である(推移性)



コメント