まだ続くベクトル空間の話。
今回はベクトル空間の定義を一般化して適用できる範囲を拡張していきます。
ベクトル空間の公理が満たされれば、例えそれがどんな風に見えてたとしても、それはベクトル空間です。
ベクトル空間の一般化
まずベクトル空間の公理から。
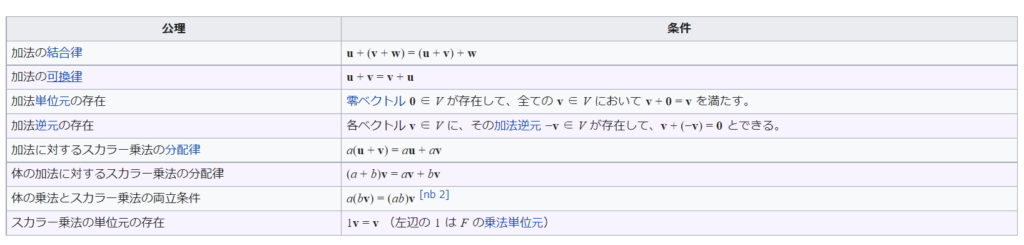
スカラー乗法の「スカラー」は実数のこと。つまり実数倍って意味です。
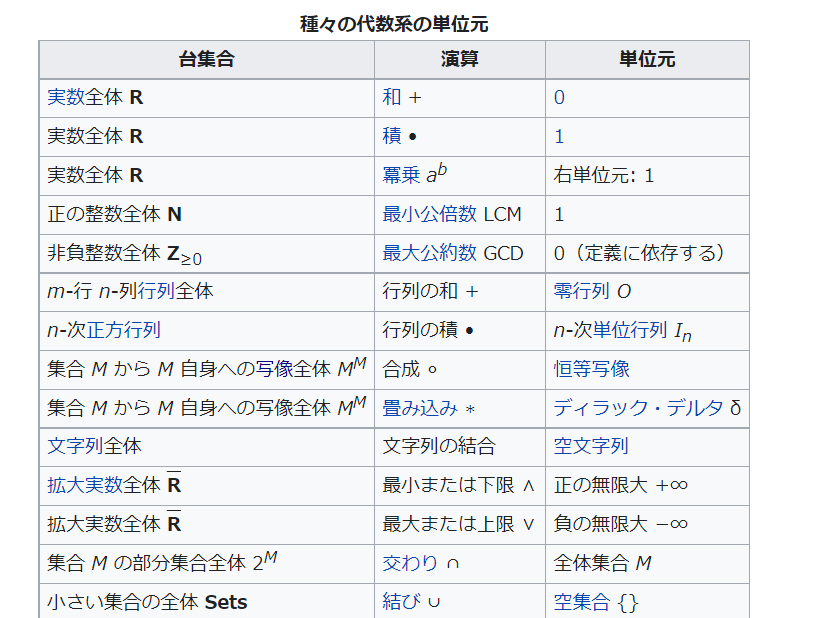
単位元は演算で何もしない元のことで、足し算なら0、掛け算なら1。
逆元はaに対する-aです。1に対する-1、1ベクトルに対する-1ベクトル。
ある集合の元において上記の公理を満たすような加法とスカラー乗法(実数倍)が定義できれば、それはベクトル空間と呼ぶことができます。
別の言い方をすれば、上記の公理は「実数における加法とスカラー乗法っぽいこと」ができるための条件を示しているんです。
ベクトル空間の加法とスカラー乗法の定義は人間が決めたものとは言え、好き勝手に定義したわけではなく、実数における加法とスカラー乗法っぽい感じになるように定義されています。
平面ベクトル
簡単なベクトル空間の例を見ていきます。
$\mathbb R^2 = \{\left(\begin{array}{c}x\\y\end{array}\right) : x,y \in \mathbb R \}$
記号は「実数の集合からテキトーに二つ取ってきて、x,yとして縦に二つ並べているよ」を意味します。
イメージだと平面のx,y軸から一つづつ点を選んで位置を特定する感じです。
平面ベクトルは二次元のベクトル空間です。
xとyの交点により表されます。
これは馴染み深いと思います。
二次元座標での加法とスカラー乗法の定義を見てみます。
太字はベクトル、普通の文字はスカラーです。
$\mathbb a + \mathbb b = \left(\begin{array}{c}a_1\\a_2\end{array}\right) + \left(\begin{array}{c}b_1\\b_2\end{array}\right) = \left(\begin{array}{c}a_1 + b_1\\b_1 + d_1\end{array}\right)$
高校数学でも習いました。
座標が同じもの同士を足すだけ。
注意点は左辺の+記号はベクトルにおける加法、右辺の+記号は実数における加法であることです。
ベクトルの加法は実数の加法で表現できますよと言っています。
次にスカラー乗法の定義。
$k\left(\begin{array}{c}a\\b\end{array}\right) = \left(\begin{array}{c}ka\\kb\end{array}\right)$
各成分をk倍します。
これらがベクトル空間の公理を満たしているのか確かめます。
まずは結合律。
(a + b) + c = a + (b + c)
a + bにcを足すのとb+cにaを足すのが変わらなければOK。
$\mathbb a = \left(\begin{array}{c}a_1\\a_2\end{array}\right),\mathbb b = \left(\begin{array}{c}b_1\\b_2\end{array}\right),\mathbb c = \left(\begin{array}{c}c_1\\c_2\end{array}\right)$
$(\mathbb a + \mathbb b) + \mathbb c = \left(\begin{array}{c}(a_1 + b_1) + c_1\\(a_2 + b_2) + c_2\end{array}\right) = \left(\begin{array}{c}a_1 + b_1 + c_1\\a_2 + b_2 + c_2\end{array}\right)$
定義通り変形します。
繰り返しですが、右辺は実数での加法です。
$ \mathbb a + (\mathbb b + \mathbb c) = \left(\begin{array}{c}a_1 + (b_1 + c_1)\\a_2 + (b_2 + c_2)\end{array}\right) = \left(\begin{array}{c}a_1 + b_1 + c_1\\a_2 + b_2 + c_2\end{array}\right)$
ベクトル加法の定義通りに変形すると(a + b) + c = a + (b + c)が論理的に同じであることが証明できました。
次に可換律。
a + b = b + a
を証明します。
$\mathbb a + \mathbb b = \left(\begin{array}{c}a_1 + b_1\\a_2 + b_2\end{array}\right )$
$\mathbb b + \mathbb a = \left(\begin{array}{c}b_1 + a_1\\b_2 + a_2\end{array}\right )= \left(\begin{array}{c}a_1 + b_1\\a_2 + b_2\end{array}\right )$
次は加法単位元。0ベクトルを定義します。
$\mathbb 0 = \left(\begin{array}{c}0\\0\end{array}\right )$
これをaベクトルに足す。
$\mathbb a + \mathbb 0 = \left(\begin{array}{c}a_1 + 0\\a_2 + 0\end{array}\right ) = \left(\begin{array}{c}a_1\\a_2\end{array}\right )$
実数の加法の0と同じものが定義できました。
次は逆元。aベクトルに対して-aベクトルを定義します。
$-\mathbb a = \left(\begin{array}{c}-a_1\\-a_2\end{array}\right)$
$\mathbb a + (- \mathbb a) = \left(\begin{array}{c}a_1 + (-a_1)\\a_2 + (-a_2)\end{array}\right) = \left(\begin{array}{c}0\\0\end{array}\right)$
次は分配律。
ベクトル同士を足した後にスカラー倍するのとスカラー倍したベクトル同士を足すのが同じであるようにとの要請を満たせるか。
k(a + b) = ka + kb
スカラーkを用意します。
$k(\mathbb a + \mathbb b) = \left(\begin{array}{c}k(a_1 + b_1)\\k(a_2 + b_2)\end{array}\right) = \left(\begin{array}{c}ka_1 + kb_1\\ka_2 + kb_2\end{array}\right)$
$k \mathbb a + k \mathbb b = \left(\begin{array}{c}ka_1 + kb_1\\ka_2 + kb_2\end{array}\right)$
定義通り変換すると$k(\mathbb a + \mathbb b) = k \mathbb a + k \mathbb b$であることが分かります。
次はスカラーを足してベクトル倍するのとスカラーをベクトル倍して足すのが同値であることを証明していきます。
スカラーa,bとベクトルvを用意します。
$(a + b)\mathbb v = \left(\begin{array}{c}(a + b)v_1\\(a + b)v_2\end{array}\right) = \left(\begin{array}{c}av_1 + bv_1\\av_2 + bv_2 \end{array}\right)$
$a\mathbb v + b\mathbb v = \left(\begin{array}{c}av_1\\av_2\end{array}\right) + \left(\begin{array}{c}bv_1\\bv_2\end{array}\right) = \left(\begin{array}{c}av_1 + bv_1\\av_2 + bv_2 \end{array}\right)$
定義通りに変形すれば同じ形にできます。
次。
スカラーをベクトル倍してさらにスカラー倍とスカラーをスカラー倍してベクトル倍するのが同値。
$a(b\mathbb v) = \left(\begin{array}{c}a(bv_1)\\a(bv_2)\end{array}\right) = \left(\begin{array}{c}abv_1\\abv_2\end{array}\right)$
$(ab)\mathbb v = \left(\begin{array}{c}abv_1\\abv_2\end{array}\right) $
同値になります。
最後はスカラー乗法の単位元について。
実数で言うところの1倍のことで、かけ算で何もしない元があることを要請しています。
1が何もしないかどうかを確かめるだけです。
$1\cdot\mathbb v = \left(\begin{array}{c}1\cdot v_1\\1\cdot v_2\end{array}\right) =\left(\begin{array}{c} v_1\\v_2\end{array}\right) = \mathbb v$
が証明できました。
空間ベクトル
$\mathbb R^3 = \{ \left(\begin{array}{c}x\\y\\z\end{array}\right) : x,y,z \in \mathbb R \}$
空間は立体なので3次元の座標で表されます。
空間ベクトルも平面ベクトルと同じ加法とスカラー乗法定義すれば公理を満たします。
ここまでは学校でやった範囲。
実n次元数ベクトル空間
次元の数を増やしても平面ベクトル、空間ベクトルと同じ論法で加法とスカラー乗法を定義でき、公理を満たすことができます。
n次元の加法の定義はこうなります。
$\left(\begin{array}{c}a_1\\a_2\\a_3\\ \vdots \\a_n\end{array}\right) + \left(\begin{array}{c}b_1\\b_2\\b_3\\ \vdots \\b_n\end{array}\right) = \left(\begin{array}{c}a_1 + b_1\\a_2 + b_2\\a_3 + b_3\\ \vdots \\a_n + b_n\end{array}\right)$
次はスカラー乗法。
$k\left(\begin{array}{c}a_1\\a_2\\a_3\\ \vdots \\a_n\end{array}\right) = \left(\begin{array}{c}ka_1\\ka_2\\a_3\\ \vdots \\ka_n\end{array}\right)$
公理を満たすかの証明は面倒なので省略します。


コメント