秩序を作ると無秩序が排出される
極限の概念を学んできて、ε – N論法、ε – δ論法などの「極限」を定義する論理はなんとか理解できたんですが、限りなく1に近づいた0.99999…は本当に1なの?ってことが置き去りだったなって感じました。
極限の定義は論理的に「限りなく近づく」を表現できてはいるけど、0.9999999999… = 1、これが正しくなかったら根本が崩壊して何のための極限だよって話になってしまいます。
直観的には0.99999… ≠ 1じゃないですか?僕はそうです。
どれだけ小数点以下の9を増やしたって1とは別物だろうって直観が働きます。
だって
1 – 0.0000000000000…1 = 1
ってことですからね?いや、違うだろと。
しかし数学では表記が違うだけの同義として扱います。
僕の直観で理解できる範囲を超えているので、論理的に0.999… = 1であることを導いてみて、自分の論理性を鍛えようと思います。
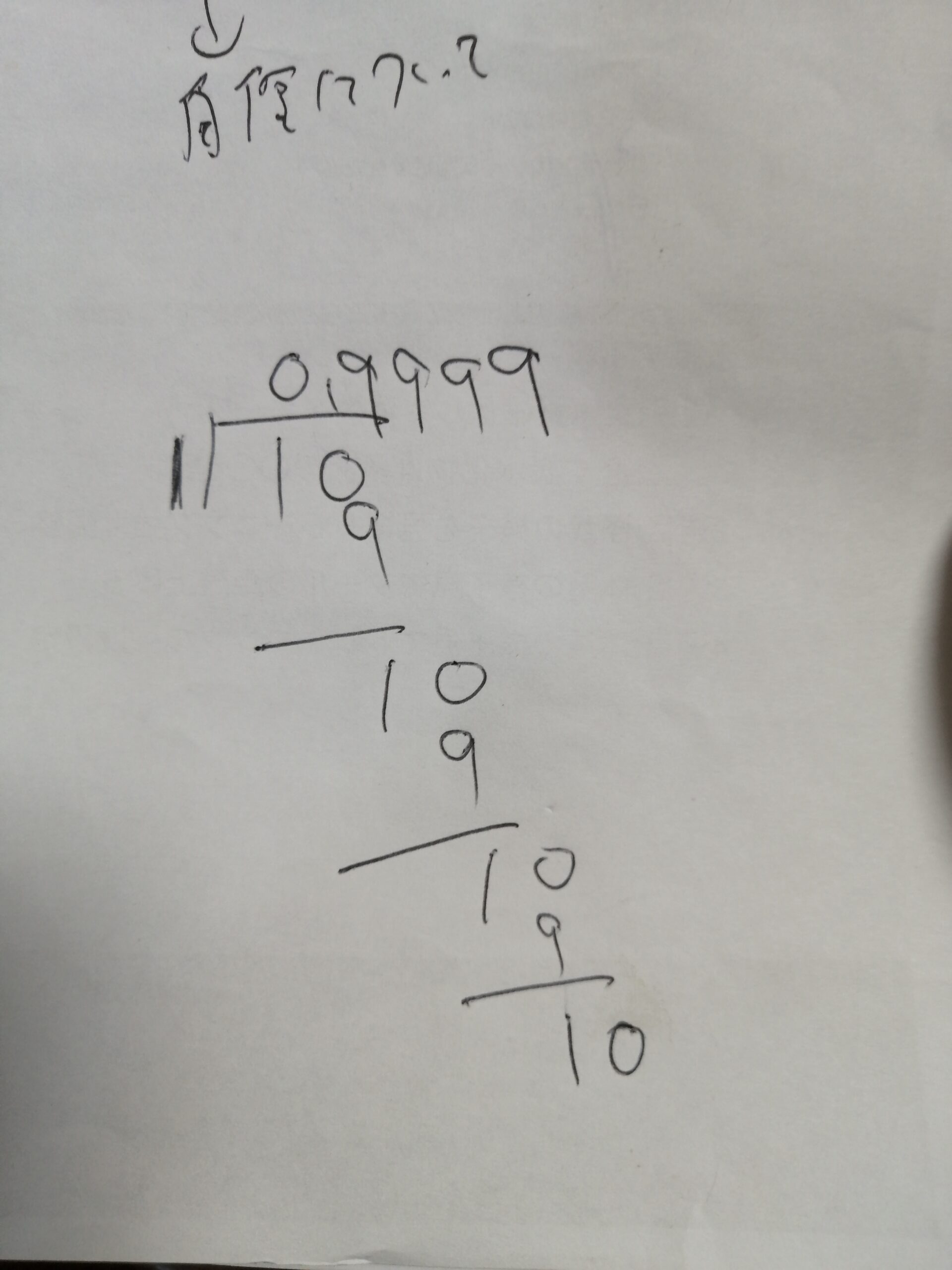
0.999=1
色んな証明があるみたいですが、これがしっくりくる。
悪筆で申し訳ないんですが、1で1を割っています。
ただそのまま割ってしまうと答えは1になるだけなので、一度目は商は立てずに少数点以下の位と一緒に割りました。
9で割って余りが1です。
0を下ろして10をまた9で割ります。
見ての通りこれって無限に続けられますよね。
1÷1 = 1 = 0.999999…
って結果を得ることができました。
直観的には別物なんですけど、論理的には同義なんですよ。
1 = 0.9999999…が論理的に同義であることは何となく理解しました。
でも今度はこんな疑問が湧いてきました。
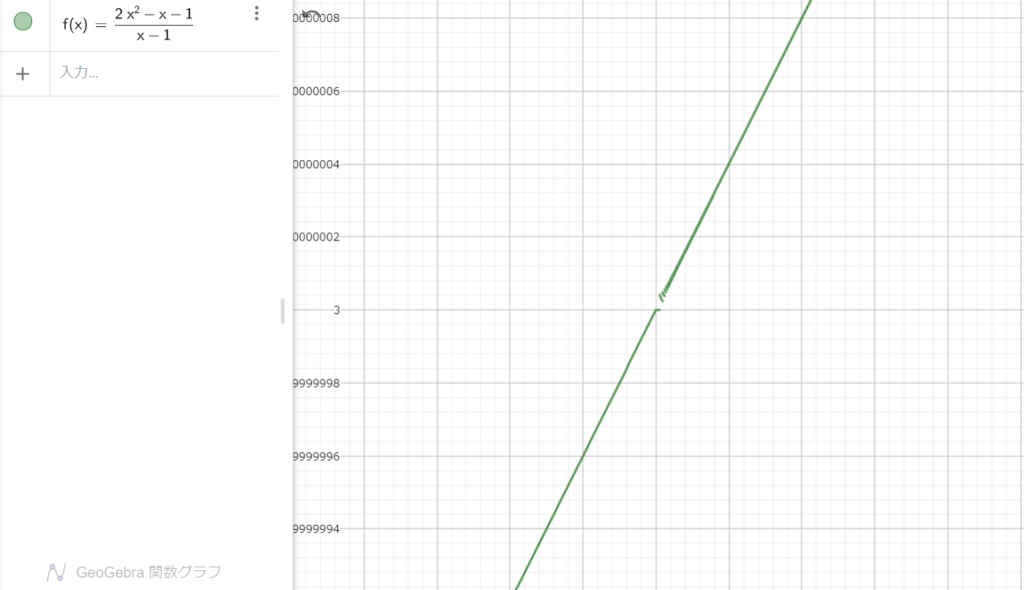
$\frac{2x^2 – x -1}{x – 1}$のグラフです。
x = 1の時には$\frac{0}{0}$になってしまい数学では定義できなくなります。
なので、x = 1の部分はぽっかりと穴が開いたようなグラフになります。
え、でもさっきの1 = 0.999999…の論理で言えば、限りなくx = 1に近づいたら(無限に拡大したら)穴はいつまでも塞がってなきゃおかしいぞって直観が働きます。
でも$\frac{0}{0}$は定義できないから穴が空いていないとおかしい。
穴が空いていて、穴が空いていない???
二つのことが同時に起こる???
これを解決する方法をちょっと考えてみたんですが、論理的には無限が”ずっとそこに在る”場合は穴は空いてません、見えません。
無限が”現れる”場合は常に穴は空いています。
多分。
「現れる」ってのは掘れば掘るほど深くなるって意味です。
ドーンと無限がそこに在るのではなく、掘り続ければどこまでも終わりなく掘ることができて、少しづつ無限が現れるようなイメージです。
現実世界に当てはまるのは後者かなあって直観が働くけどどうだろう。
数学や物理学では果てしなく続く無限とその始まりとなる起点をどう定義しているんだろう。
この話って「宇宙は最初からそこにあった」、「無から何かをきっかけに生まれた」って議論の奇妙さと同じです。
始めからそこに在ったとしても無から生まれたとしても発生の原因が存在しないことになります。
僕達の存在ってどうやって証明するの?因果関係を証明できないの?そんなに脆弱なの?って思いませんか?
二つのことが同時に起こるのは「波と粒子の二重性」「非実在性」を扱う最先端の物理学、量子力学でも議論されていますよね。
無限に小さくしていくと因果関係の論理が崩壊する。
人間の論理が通用しないだけなのかもしれませんが、なんだか世界って奇妙だと思いませんか。


コメント