 暇つぶしに見て
暇つぶしに見て 同型写像って何やねん
続き。 同型写像 2つの数学的対象が同型 (isomorphic) であるとは、それらの間に同型写像が存在することをいう。自己同型写像は始域と終域が同じ同型写像である。同型写像の興味は2つの同型な対象は写像を定義するのに使われる性質のみを使...
 暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て 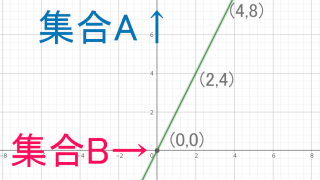 暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て