循環小数ならば有理数
循環小数(じゅんかんしょうすう、英: recurring decimal、repeating decimal)とは、小数点以下のある桁から先で同じ数字の列が無限に繰り返される小数のことである。繰り返される数字の列を循環節という。
有理数(ゆうりすう、英: rational number)とは、整数の比(英: ratio)として表すことができる実数のことである。
11/3=3.666…
1/3=0.333…
5/7=0.7142857142857…
繰り返しの節は「循環節」と呼ばれます。
小数点以下が循環節だけになるまで10ⁿ倍します。例えば上の例なら
10¹×3.666…=36.666…
10¹×0.333…=3.333…
10⁶×0.7142857142857…=714285.714285…
さらに、その値から10^m倍を引けば小数点以下が消去されて整数になります。
36.666…-3.666…=33
3.333…-0.333…=3
714285.714285…-0.714285=714285
任意の循環小数xを10ⁿ倍し、そこから10^m倍を引けば整数yとなります。
(10ⁿ-10^(m))x=y
x=y/(10ⁿ-10^(m)
yは整数。整数の整数倍は整数。また、整数同士の差は整数。整数は有理数。すなわち
y/(10^(n+m)-10ⁿ)
は有理数。
同値関係より、循環小数のxは有理数。
下の記事の証明を合わせると
循環小数⇒有理数
有理数⇒循環小数
有理数⇔循環小数
無理数=¬有理数
関連記事


有理数×無理数=無理数
有理数の加法と乗法は定義より
有理数×有理数=有理数
有理数+有理数=有理数
となります。つまり有理数の演算は閉じています。
有理数×無理数=有理数
だと仮定します。
無理数=有理数/有理数
無理数=有理数
以上は有理数の演算が閉じている要請を満たしていません。矛盾します。背理法により¬有理数を導出できます。
実数は有理数か無理数に分類されます。
¬有理数=無理数
有理数×無理数=¬有理数
有理数×無理数=無理数
となるので有理数と無理数の演算は無理数となります。
関連記事



-の性質
0=-0とx×0=0の定理を用います。
x×(-0)(前提)
x×0(同値変形)
0(乗法定理)
x+(-0)(前提)
x+0=x(-0=0)
x+(-0)=x(推移律)
0+(-x)(前提)
-x+0(加法4)
-x(加法2)
0+(-x)=-x
関連記事


三角錐の体積
引用した本に体積を求める練習問題があります。が、僕は義務教育でやったのしか覚えとりませんので躓きました。というわけで頭の整理も兼ねて中学の復習。
四角形の面積は
縦×横
直感的に横の長さの直線を縦の長さ分だけ積み重ねたのが四角形の面積であると理解できます。
四角柱の体積は
底面×高さ
四角形を高さ分だけ積み重ねたのが四角柱。
円柱
半径×半径×π×高さ
円を高さ分だけ積み重ねたのがが円柱の体積
では三角錐や四角錐や円錐は?
三角錐(さんかくすい、英語: triangular pyramid、trigonal pyramid)や四面体(しめんたい、よんめんたい、英語: tetrahedron)とは、垂直断面に三角形を持つ錐体のことである。辺6本、頂点4つからなる。面の数は立体に於ける最小限界の4つであることから四面体とも呼ぶ。三角錐は、最小の頂点数で構成することができる立体であると表現することもできる。
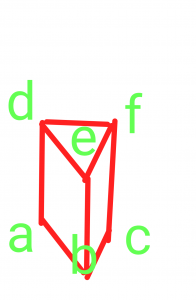
三角錐を考えます。
※三角柱ではない
それは最小の点と面で構成される立体。四面体。
底面を△abcとする三角柱abcdefを考えます。
△abcとdを結ぶ三角錐Aをその中にいれます。次に△defとcを結ぶ三角錐Bをいれます。あまった部分へ△dbeとcを結ぶ三角錐Cをいれます。
(△abc≡△def)∧(af=cf)
底面と高さが同じなので、二つの三角錐AとBは合同と仮定します。
※合同の厳密な定義を調べるのが面倒なので、それは一旦は無視し、我流で合同であると認めてしいます。
次に余りの△dbeとcで構成される三角錐Cを考えます。
三角錐AとCの底面を□abedとして考えます。対角線dbで分割した△abdと△bedは高さと底辺が同じ。つまり、三角錐AとCの底面は合同。
また、三角錐AとBを構成する残りの点は同じbc=bc。高さを構成する辺と面が合同。すなわち三角錐を構成する面が全て合同。よって三角錐AとCは合同。図形の同地関係が成り立つと仮定するならA≡B≡C。
三角柱の中には同じ大きさの三角錐が3つ隙間なくギチギチに敷き詰められます。従って、その三角柱abcdef を三分割したものが一つの三角錐の体積となります。
(底面×高さ)×1/3
ひとまずはこれで納得します。

コメント