実数乗法の0

二行目と四行目は実数から0(加法単位元)を引いた差集合として演算が定義されています。何故だろうかと。
二行目は、かけると元の数になる乗法単位元の存在の要請です。
0×∀x∈ℝ=0
0は何倍しても0であってほしい。
この要請は0に対しては全ての実数が単位元の役割を果たしてしまうことになる。定義に0を含めると単位元が厳密には単位元として機能しない。だから0を除いた。
次は三行目。これは任意の元に対する逆元の要請。
この規則を0に当てはめてしまうと
0×0⁻¹=1(R3)
0は何倍しようが0であってほしい、というヒトの認識の要請と適合しません。

x+y=z⇔x=z+(-y)
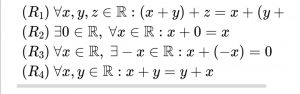
x+y=z(前提)
x+y+(-y)=z+(-y)(加法一意性)
x=z+(-y)(R3)
移行できる、あるいは減法へ変形できる、と言い換えられると思います。
下の引用で証明した実数加法の一意性を応用し、同じ値を足した場合は関係が変化しない性質として利用しました。
x+y=x+z→y=z
y=z→x+y=x+z
x+(-y)=x-y
とするなら減法。

x×y=z⇔x=z×y⁻¹
x×y=z
x×y×y⁻¹=z×y⁻¹
x=z×y⁻¹
これも同じようにしたで証明した実数乗法の性質を用いました。
x⁻¹=1/x
とするなら除法。あるいは移項。

x×(y+z)=x×y+x×z
分配法則。
x×(y+z)=x×w
y+z=w
()を外して分配したかったのですが、実数の乗法と加法を結びつける方法が思いつきませんでした。
グーグル先生によれば、二つを繋ぐ分配法則は定理ではなく定義とのこと。またそれで創り出した集合を「環」と呼ぶとのこと。
数学における環(かん、英: ring)とは、台集合に「加法」(和)および「乗法」(積)と呼ばれる二種類の二項演算を備えた代数系のことである。
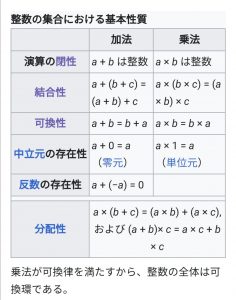
最もよく知られた環の例は、整数全体の成す集合に自然な加法と乗法を考えたものである(これは乗法が可換だから可換環の例でもある)。
最後に分配法則の定義があります。
x×0=0
x×0=0
は実数の乗法には定義されていまません。でも、人の認識としては無(0)に何を作用させても無(0)であってほしい。
x+y=x+z⇒y=z
下で証明した実数加法の一意性の性質。

0(前提)
0+0(加法2)
0×1+0×1(乗法2)
0×1+0×1=0+0(同値関係)
0×1=1×0=0(乗法5)
x×0(前提)
x(0+0)(加法2)
x×0+x×0(乗法5)
x×0+0=x×0+x×0⇒x×0=0(実数の一意性)


コメント