頭の体操七

暇つぶしに見て

2024.12.022024.12.03

逆元の逆元

-(-x)は逆元の逆元という意味。裏の裏は表、の証明。

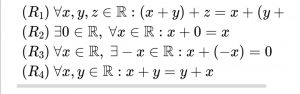
公理主義実数論の公理から。
∀x,∃-x∈ℝ:x+(-x)=0

任意の元xを選ぶとその逆元は必ず存在します。
(-x)+(-(-x))=0(R3)
-(-x)+(-x)=0(R4)
x+(-x)=0(推移律)
-xを選んだ場合、その加法の逆元は、xになることを示しています。裏の裏は表、みたいなこと。

実数加法一意性

x+y=x+z→y=z
の証明。

x+y=x+z(仮定)
y=y+0(R2)
y=y+x+(-x)(R3)
y=x+y+(-x)(R4)
y=x+z+(-x)(同値変形)
y=x+(-x)+z(R4)
y=0+z(R3)
y=z+0(R4)
y=z(R2)
x+y=x+z→y=z(→導入)

加法の一意性が証明されました。

=は引用では具体的には定義されていませんが、記述の仕方から同値関係の推移律対象律反射律が成り立つものとして仮定しています。

0(前提)
0+(-0)=0(R3)
(-0)+0=0(R4)
-0=0(R2 )

実数の加法において、0とその逆元-0は同値であることが証明されました。

実数 $x$ の正整数 $n$ 乗は、素朴には、 $n$ 個の $x$ を掛け合わせたものである。厳密には、次のように再帰的に定められる。

(*)x1:=x, (**)xn+1:=xn\timesx(n\geq1). ウィキペディア

2²(前提)
2¹×2(∗∗)
2×2(∗)
4(乗法定義)
を満たすような規則が定義されています。

n=0にも定義が適用できると仮定して(n≥1).を無視します。

x⁰(前提)
x^(0+1)(∗∗)
x¹=x⁰×x¹(∗)
1=x⁰(約分)

定義から演繹的に求めるなら、xの0乗は1となります。