最近、論理パズルにハマっています。
良い問題なら一問で数時間、数日遊べるのでコスパ最強ですよ。紹介した書籍にはそれが何十問もあります。で、数百円。
居酒屋で酒を飲むより、漫画を買うより、遥かにコスパが良い。しかも論理性も鍛えられる。
遊戯王にハマった、将棋、チェス、麻雀などの論理パズルを組み立てるのが好き、ならずっと遊べると思います。
紹介した書籍の難しい問題は本当に難しい。でも、思考の奥行きがかなり広がりますよ。
今回は3×3魔法陣。これは石碑として発見されるなど、歴史的にはかなり古くから好まれていた遊びであるようです。
魔方陣の歴史は古く、中国では紀元前190年前には存在していた。魔法や神話的な意味を獲得し、芸術作品の象徴として様々な場所で用いられてきた。 現代では縦・横・対角線以外の形状の和や、数字の積などの単なる和以外の演算などにも一般化されている。
ルールは単純。タテ、ヨコ、ナナメ、三マス8通りの和が全て15になるような組み合わせを探すだけ。
ルールだけならば小学生でも理解できる単純さです。が、本気で知恵を絞らなければ答えにはたどり着けません。
前提①タテヨコナナメ三マスの合計は常に15。
では始めます。
abc
def
ghi
ナナメ
a+e+i
タテ
b +e+h
ナナメ
g+e+c
この組み合わせから
ヨコ
a+b+c
g+h+i
の二通りを引けば、eが3つと15だけが抽出されます。
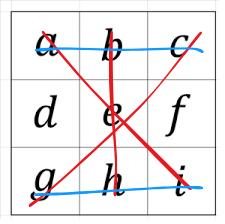
分かりやすく上の論理を図にしました。
赤線のタテナナメの三つの組み合わせから青線の組み合わせを引くと、eが三つだけ抽出されます。
また前提より、赤線から青線を引いた場合は
15×3-15×2=15
となります。
式にすると
(a+e+i+b+e+h+g+e+c)-(a+b+c+g+h+i)
=3e=15
e=5
e=5①が決定。
次に「1」を収める場所を探します。
a=1と仮定すると前提①よりi=9となります。
この場合は1行目の組合せは
1+b+c=15となり
b=8,c=6またはb =6,c=8となります。
この場合はc+f+9=15を満たささず前提①と矛盾。
a≠1は決定。
abc
def
ghi
を右へ反時計回りに一回転させることを2Rと表わします。2Rは
cfi
b5k
adg
この場合にa=1を選ぶとaeiは159となり、先程の偽となった1Rと同じ組合せとなり同値関係。
同様に1R=2R=3R=4Rとなることが言えます。
したがって四隅の数が1と9ではないことが確定しました。
9∨1≠a,c,g.i
1と9が四隅と中央ではない。
すなわちb=1,h=9②が決定。
また、三マスを合計して15となる規則から、a=8,c=6またはa=6,c=8が決定します。
a=8と仮定③
この場合は
a+e+i=15
=8+5+i=15
となるので、i=2が決定。
また
g+h+i=15
=g+9+2=15
g=4も決定。
これにより
a+d+g=15
=8+d+4=15
d=3も決定。
最後は
3+5+f=15
f=7
816
357
492
タテヨコナナメの三マスの和が全て15になります。
やった!完成!もう少しスマートな方法があるかもしれませんが、とりあえず今の実力はこんなもん。
次は4✕4に挑戦します。
組み合わせの考え方や論理的な推論が遊びながら自然に身につくので、娘が成長したら一緒にやりたい。


コメント