必要十分条件と集合と同値関係

定義は定義として受け入れるとして、その心が知りたくなるのが人情。
十分条件と必要条件を定義に背後にある心を考察していきます。

必要十分条件と同値関係

必要十分条件と同値関係

必要十分条件

というわけで十分と必要の日本語から。

【十分・充分】
《ダナノ・副》
物事が満ち足りて、何の不足もないさま。
「―な手当」
Oxford Languages

【必要】
《名ノナ》
かならず要(い)ること。なくてはならないこと。
Oxford Languages

必要十分条件
二つの条件 p 、q に対して、「 p を満たすものは全て q も満たす」というとき、「 p は q である為の十分条件である」あるいは「 q は p である為の必要条件である」という。
また、「 p は q である為の十分条件であり、q は p である為の十分条件である」というとき、「 p は q である為の必要十分条件である」あるいは「 p と q とは同値である」という。
Wikipedia

「十分」は日常の意味通り、それだけで条件を満たすことができること、つまり命題pの真と同時に命題qも成立してしまうこと。
一方で「必要」は命題pが真となることだけでは「十分」ではなく、他の要件もある、というようなことかと。

両方向から十分条件が成立した場合が必要十分条件。

論理包含の真理値表

[table id=implication /]

「 p を満たすものは全て q も満たす」
は
p→q
の式で恒にpが真の場合を意味します。
真理値表を見ると、pが真で論理包含の結果も真となるのは一つだけ、qが真の場合のみです。つまり、pが真ならば必然的にqは真になるわけです。だから十分条件。

一方でqが真の場合は真理値表を見るとpが偽の場合でも演算結果は真となります。必要な条件ではあるけど、それだけでは十分と言えません。だから必要条件。

論理包含と集合

【具体例】
$x=2→x^2=4$
$x=2$は$x^2=4$の十分条件となります。
$x^2=4$は$x=2$の必要条件。

$x=2$が真であれば$x^2=4$は真しかあり得ません。
$x^2=4$が真でも$x=2$とは限りません。$-2$があります。

ここで集合っぽいものが浮かび上がってきます。
わかりやすく真理値表で考えます。
p→q
この式が恒真式であるなら、pを真と仮定した場合（一通り）の集合はqを真と仮定した場合（二通り）の部分集合と見ることができます。

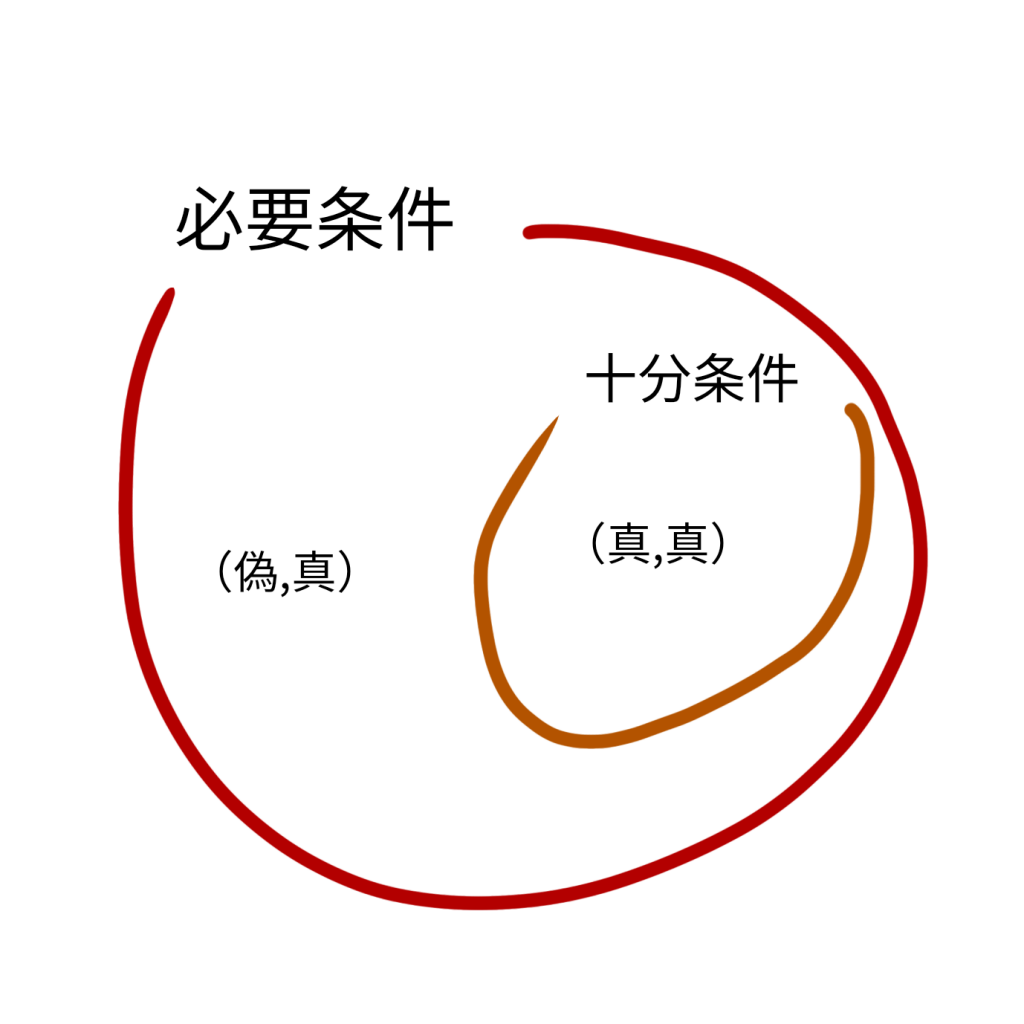
同値までが見えて来ました。

必要十分条件と同値類

必要十分条件が同値と定義されています。
つまり集合がピッタリと重なった時、論理包含が両方向に成立するa⇔bの場合を同値と呼ぶ、ということですね。

なるほど、この文脈から読み解くなら、同値類を定義する反射律や推移律、も理解できそうな気がします。
集合は存在を定義する部品を集めてきたものと解釈することができますから、長濱陸の条件の集合と一致する集合があるなら、されは論理包含という文脈から同値だと判断できます。

同値関係の疑問が解消されてきました。

ある集合 S において、以下の3つの性質をすべて満たす二項関係 ∼ は S 上の同値関係であるという。
それらの性質とは S の任意の元 a, b, c に対して、反射律: a ∼ a.
対称律: a ∼ b ならば b ∼ a.
推移律: a ∼ b かつ b ∼ c ならば a ∼ c.
Wikipedia