自然数に続いて整数の定義しようと思ったら、そのためには同値類という集合の分類を定義する必要があり、さらにそれを定義するためには直和と直積という定義を学ばなきゃならんようなんで、やっていきます。
直積、直和という概念は物理学にも応用されているとても重要な概念なんだそうです。
数学の抽象的な論理の探求が具体的に現実を記述する量子力学における議論を予言していたって考えると、数学って面白いな、凄いなって感じますよね。
直和と直積
和集合
直和は和集合の一種ということなんで和集合から。
定義がこんな感じ。
定義
Wikipedia
集合 A と集合 B が与えられたとき、集合 A ∪ B を、A, B いずれかの集合の少なくとも一方に含まれる元 x の全体 (x ∈ A ∪ B ⇔ x ∈ A または x ∈ B) として定めて、あるいは同じことだが
$A \cup B := \{x | x \in A \ or \ x \in B \} $
として定義される集合を、集合 A, B の和集合と呼ぶ。また特に、A と B が交わりを持たないときの和集合 A ∪ B を A と B の(集合論的)直和(ちょくわ、[set theoric] direct sum)あるいは非交和(ひこうわ、disjoint union)と呼び…

このイメージが和集合。
AとBのすべての元を束ねたものが和集合で、後述しますがこの時AとBが交わりを持たない場合は直和となります。
積集合
定義
Wikipedia
集合 A, B の交わりは A ∩ B と記される[4]。これは
x ∈ A ∩ B ⇔ x ∈ A かつ x ∈ B
ということであり、記号ではA ∩ B = { x | x ∈ A∧x ∈ B }
と書ける。A ∩ B に含まれるような元が存在するとき A と B とは互いに交わるあるいは交わりを持つといい、そのような元の存在しないとき A と B は互いに素であるまたは交わりを持たない (disjoint) という。

イメージこんな感じ。
灰色の部分が積集合です。
直和
既知の数学的対象を「貼り合わせ」て同じ種類の対象を新たに作り出す操作の一種
Wikipedia
歴史的経緯から対象によってやや異なる意味で用いられるが、大雑把には集合論的、代数学的、圏論的用法に大別できる。
概要はこんな感じで分かりやすいのですが、定義の仕方は集合論、圏論、代数学などそれぞれの分野によって異なる手法をとっているみたいです。
素人の僕が全ての定義を厳密に理解しようとすると整数って概念を学ぼうって最初の方針から大きく脇道へ逸れてしまうので、僕なりの理解で直和について解説します。
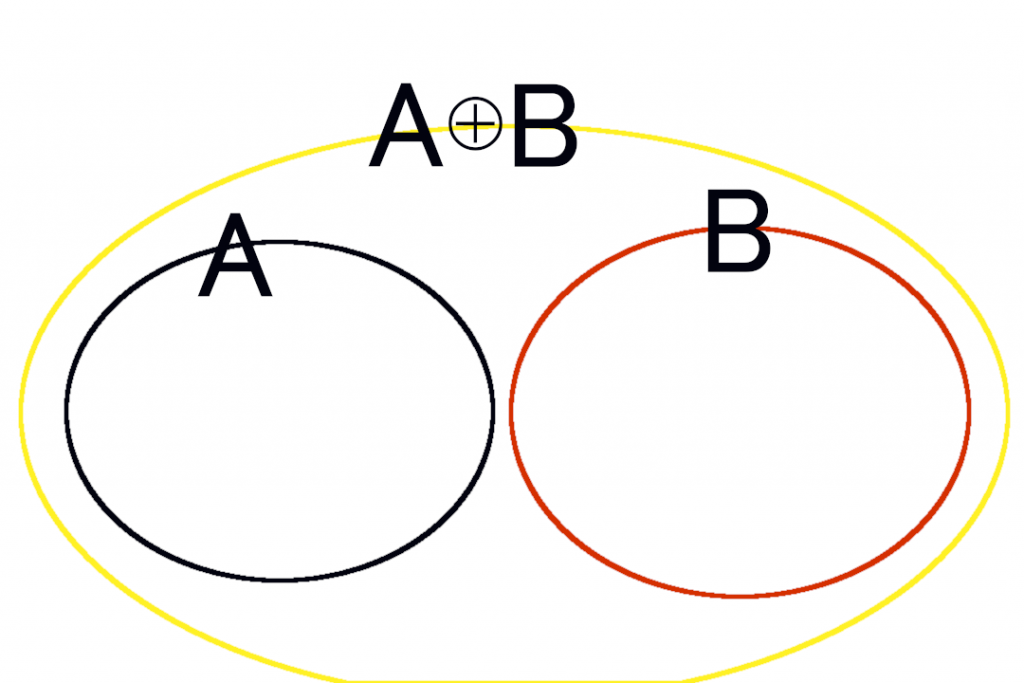
集合論的な直和のイメージは多分こんな感じ。
定義は上の和集合、積集合を用いてこんな感じ。
至ってシンプルです。
定義
$A \cap B = \varnothing$
$A \coprod B:= A \cup B$
2行目の左辺は直和を表す記号で、「:=」は左辺で右辺を定義することを意味しています。
まとめると、「AとBの積集合が空集合である時にAとBの和集合がAとBの直和になる」です。
線形代数学ではさらに
定義
$A \cap B = \varnothing$
$A \coprod B:= A \cup B$
集合A,Bの任意の元(ベクトル)が垂直に交わるような空間で
$A \oplus B$
と表す
以上を「直和空間」と定義するようですね
集合論の直和の意味をより深めて、ベクトル空間に応用できるように拡張したような定義になっています。
こっちの方はイメージが平面や立体に広がってくので直和の意味が分かりやすい気がします。
例
※直積を勉強している最中に気が付きましたが、例えに微妙な変更があります。
例えばどんなものがあるだろうかと探してみたんですが、最も分かりやすい直和の例は二次元直交座標でしょうか。
x軸の位置ベクトルの大きさは色々なものがありますよね。
y軸の位置ベクトルも然り。
それらをXとYの集合を定義して
$X \cap Y = \varnothing$
とします。
これは線形独立なのでxy二次元直交座標が集合x,yの直和となることを意味します。
$A \oplus B = V$と定義してVから元をテキトーに一つとってくると
$v \in V$は$a \in A,b \in B,v = a + b$、つまりxy座標で一意に表現できます。
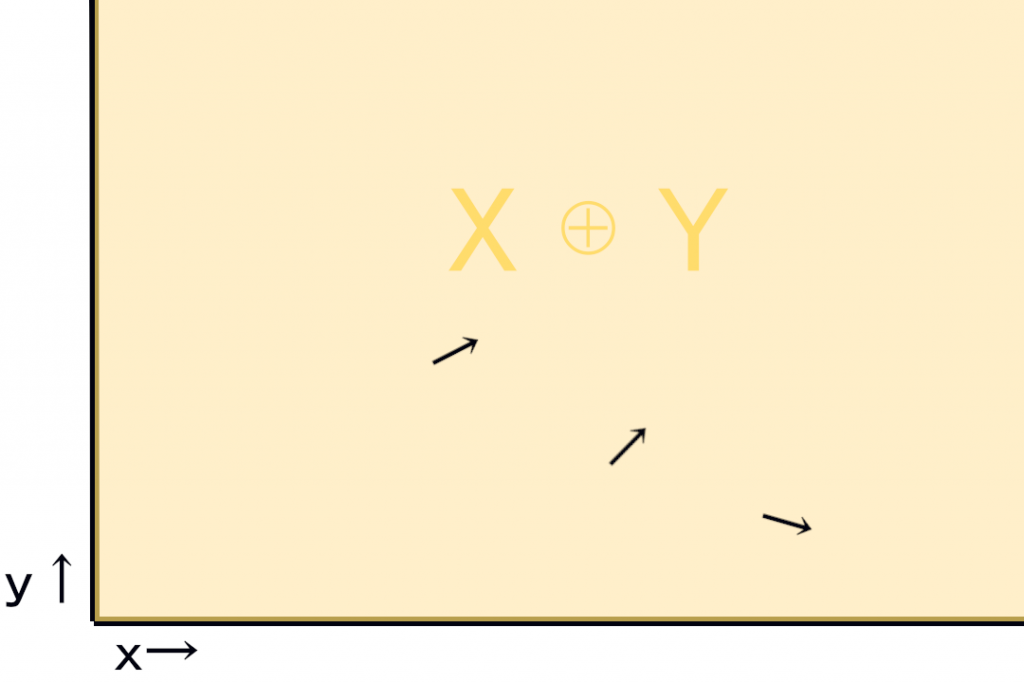
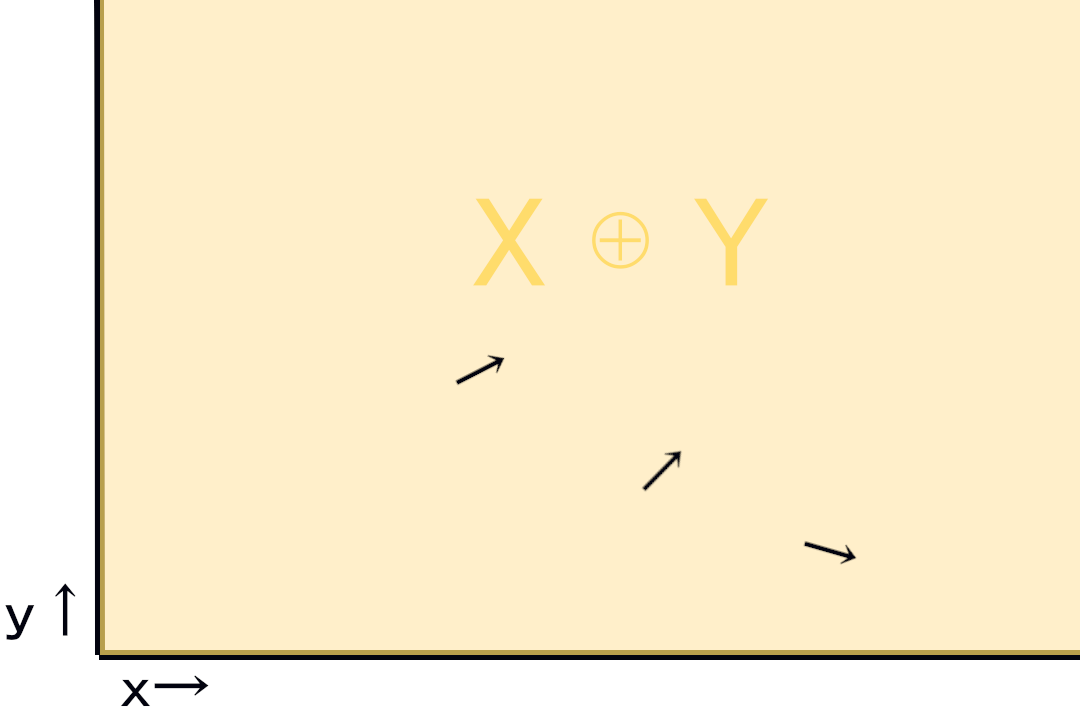
線形代数学の直和空間のイメージは多分こう。
x軸,y軸が集合でその直和が黄色の部分。
黄色(直和空間)の中にある黒いベクトルはx,yの元の和で一意に表せます。
※ここまで直積のイメージです悪しからず。
奇数と偶数の直和は自然数。
これも一例だと思います。
何故このような概念が必要なのかは全く掴めず、まだまだイメージだけの漠然とした理解なんですが、完璧に理解しようとすると寿命が来ちゃうんでひとまずはこの程度の理解で進めていき、必要なら都度更新していくスタイルでやります。
まずはイメージだけ抑えて、直和の威力が現実のどの議論で有効なのかは今後勉強しながら理解できればと思います。


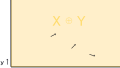
コメント