素人が数学に挑戦線形変換

行列の和は成分同士を足し合わせるだけなのでベクトル加法のイメージを広げることで理解できました。ただ行列の積は独特な演算規則が定義されていてすんなりとは理解できません。
理解するのにかなり苦労したんですが、ようやく何となく行列が何なのか、何故行列積の定義があのように意味不明な定義をされているのか分かってきました。

線形性、線形写像て所から始めると行列が理解しやすすかったので、そこから話を進めていこうと思います。

線形変換

線形変換

線形性

平面上の直線が、この直線上に原点をもつ(x,y)座標で、二つの変数xとyの同次一次式で表されることからこの名が生まれた。
コトバンク

同次とは$x^2 + y^2 + z^2$のよう次数が揃っているもの。
一次式は次数が一つ$x + y + z$のようなもの。
グラフの座標は平面の点なら(1,2)で平面ベクトルx + yなら,空間の点なら(1,2,3)でベクトルならx + y + zという風に表せます。

四次元以上の直線はちょっと僕の脳みそではオーバーフローしてイメージができませんが、論理的には記述できます。無理やり想像すると、三次元空間が縦か横に無限に重なった感じかなと。
五次元だと三次元が縦と横と高さの立体構造（大きさはない？）に押し込められた感じでしょうか。
六次元は…五次元をすっぽり内包するような極限まで圧縮された薄い層が幾層も重なっている感じかな…ちょっと想像を超えます。

閑話休題。
線形性とはその名の通り直線、要するにベクトル（座標）です。

次数の多い曲線でも微分を繰り返せば直線に変形できるので、微分も線形性との関連が深そう。

基底ベクトル

余談
行列積の規則を理解する上で「基底ベクトル」を知ってると理解しやすかった。

基底ベクトル
線型代数学における基底（きてい、英: basis）とは、線型独立なベクトルから成る集合あるいは組で、そのベクトルの（有限個の）線型結合として、与えられたベクトル空間の全てのベクトルを表すことができるものを言う。
Wikipedia

初耳の用語が出てきて意味が分からんので、まずは初耳の奴らからやっつけます。
まずは線形独立。

線形独立
線型代数学において、n 本のベクトルが線型独立（せんけいどくりつ、英: linearly independent）または一次独立であるとは、それらのベクトルが張る空間が n 次元部分線形空間になることである。
Wikipedia

要するに軸のことですね。
2本なら平面を張り、3本なら立体を張ります。

線形結合
線型結合（せんけいけつごう、英: linear combination）は、線型代数学およびその関連分野で用いられる中心的な概念の一つで、平たく言えば、ベクトルの定数倍と加え合わせのことである。一次結合あるいは線型和とも呼ぶ。
Wikipedia

ベクトルの加法とスカラー乗法のことです。

以上踏まえた上で基底ベクトルを訳すと。
「n次元ベクトル空間からn個のベクトル（線形独立）を選び、それらのベクトルの加法とスカラー乗法でn次元ベクトル空間の中にあるすべてのベクトルを表現（線形結合）できる場合、それは基底ベクトルだよ」です。
もっとかみ砕くと「軸が基底ベクトルだよ」です。2次元ならx,yが、3次元ならx,y,zが基底ベクトルです。

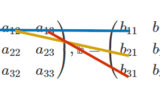
黄色と紫が基底ベクトルです。
これらのベクトルのスカラー倍と加法で青いベクトルを表現できます。
仮に青がどんな大きさ、向きだったとしても黄色と紫のベクトルだけで表現できます。

つまり基底ベクトルです。

注意点は基底ベクトルは線形独立であれば、どの方向を向いていても構わないことです。

二次元を表現する場合、線形独立な二つのベクトルであれば、こんな風に傾いていても、スカラー倍と加法で青いベクトルは表現できます。

つまり、n次元の平面を表す基底ベクトルの組み合わせは無限に存在しています。

線形変換（線形写像）

前置きはこの辺にして行列を掘り下げて行列積の定義の理由を見ていきます。

線形（ベクトル）変換という側面から行列積を見ていきます。

適当なベクトルを作ります。
$\begin{pmatrix}1\\ -4\end{pmatrix}$
このベクトルは2次元座標なので平面ベクトル。

これに２×２の行列を定義通り乗算します。
$\begin{pmatrix}2 & 2 \\ 3 & 3 \end{pmatrix}\begin{pmatrix}1\\ -4\end{pmatrix} = \begin{pmatrix}-6 \\ -9\end{pmatrix}$
次元の数は同じままでベクトルの各成分が乗算の前後で変わりました。
「行列はベクトル（線形性）に作用（掛ける）して別のベクトルを生成する」とも換言できます。
ベクトルに行列をかけると別のベクトルへ変換されるので「線形変換」と呼ばれています。

グラフで見てみると分かりやすくなります。

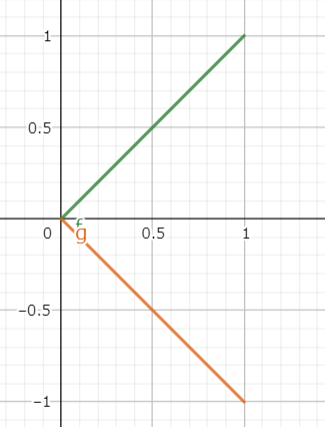
緑のベクトル$\begin{pmatrix}1 \\ 1\end{pmatrix}$をオレンジのベクトル$\begin{pmatrix}1 \\ -1\end{pmatrix}$に変換する行列は$\begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}$になります。

行列の規則通りに乗算してみます。
$\begin{pmatrix}x’ \\ y’\end{pmatrix} = \begin{pmatrix}1 \\ 1\end{pmatrix}\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix} = \begin{pmatrix}1 + 0 \\ 0 +(-1)\end{pmatrix}=\begin{pmatrix}1 \\ -1\end{pmatrix}$
行列を掛けることでベクトルがx軸を対称に反転しました。

他の似たような行列$\begin{pmatrix}1 & -1\\0 & 0\end{pmatrix}$をかけるとどうなるか。試しにやってみます。

$\begin{pmatrix}x’ \\ y’\end{pmatrix} = \begin{pmatrix}1 \\ 1\end{pmatrix}\begin{pmatrix}1 & -1 \\ 0 & 0\end{pmatrix} = \begin{pmatrix}1 + -1 \\ 0 + 0\end{pmatrix}=\begin{pmatrix}0 \\ 0\end{pmatrix}$
0ベクトルに変換されました。

行列をベクトルに入力すると別のベクトルへ変換されることが分かりました。
そして、同時に思い出してほしいのが写像。集合の元と別の集合の元へ結びつける規則が写像でした。
行列は集合（ベクトル空間）から集合（ベクトル空間）への対応関係なので、写像だと言えます。

ここまでくるとなぜ行列積の定義がややこしいのかをフワフワとですが、理解できてきました。

行列同士の積の規則

行列はベクトルを別のベクトルへ変換する写像なんです。
既述の基底ベクトルを思い出してください。
n次元ベクトル空間におけるn個の線形独立なベクトルは、それらの足し算とスカラー倍だけでn次元ベクトル空間内のすべてのベクトルを表現できます。
先ほど行列はベクトルを変換することだと解説したように、基底ベクトルに作用させる行列次第でどんなベクトルでも表現できるんです！

具体的に見ていきます。

n次元ベクトル空間V,Wを用意します。
基底ベクトルを$\{v_1,v_2,\cdots v_n\},\{w_1,w_2,\cdots w_n \}$とします。

この時基底ベクトル$\{w_n\}$は$\{v_n\}$の線形結合（スカラー倍と足し算）を用いて
$w_1 = a_{11}v_1 + a_{21}v_2 + \cdots a_{n1}v_n$
$w_2 = a_{12}v_1 + a_{22}v_2 + \cdots a_{n2}v_n$
$\cdots$
$w_n = a_{1n}v_1 + a_{2n}v_2 + \cdots a_{nn}v_n$
と表せます。

これって行列積の規則そのものですよね。
行列はベクトルを変換する写像なんです。
基底ベクトルから別の基底ベクトルへの変換は上記の規則に沿って行われます。
行列はその規則を含めたすべてが線形変換のための一つの処理になっているんです。

行列に直すとこうなります。行列aをベクトルvに作用させてベクトルwを作り出します。
基底ベクトルを別の基底ベクトルへ変換させる作業が行列積だと考えると理解しやすいです。
$\mathbb W = \begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix} \begin{pmatrix}v_1 \\ v_2 \\ \vdots \\ a_n\end{pmatrix} = \begin{pmatrix}a_{11}v_1 + a_{21}v_2 + \cdots a_{n1}v_n \\ a_{12}v_1 + a_{22}v_2 + \cdots a_{n2}v_n \\ \vdots \\ a_{1n}v_1 + a_{2n}v_2 + \cdots a_{nn}v_n \end{pmatrix}$

行列の積の定義
$\mathbb{ab} = \begin{pmatrix}a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31}& a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32} & a_{11}b_{31} + a_{12}b_{32} + a_{13}b_{33}\\ a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31}& a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32} & a_{21}b_{31} + a_{22}b_{32} + a_{23}b_{33} \\ a_{31}b_{11} + a_{32}b_{21} + a_{33}b_{31}& a_{31}b_{32} + a_{32}b_{22} + a_{33}b_{32} & a_{31}b_{31} + a_{32}b_{32} + a_{33}b_{33} \end{pmatrix}$

高校でいきなり「行列」って意味不明なものをドーンって渡されて、これまたよく分からない規則を覚えさせられて混乱しましたよね。あの時に先生が行列によってグラフのベクトルが変換されるイメージだけでも教えてくれたら「なるほど、ベクトルを変換するものが行列なのか」と少しは納得できたと思います。
プレステも64も使い方分からなかったらただのプラスチックの箱です。面白さなんてありません。