前回は「ボルツァーノワイエルシュトラスの定理」ってかっこいい定理を学びましたが、今回は「コーシー列」。ガノンドロフ、ビーフストロガノフ並みに強そうな名前です。
コーシー列
コーシー列のイメージ
コーシー列は極限をとると点と点の幅が小さくなっていく数列です。
Wikipediaから引用します。

この数列はnが小さいうちはポツポツと点が並んでいますが、nが大きくなってくると徐々に振動が小さくなって点が集まっていきます。
これがコーシー列です。
Wikipediaによると別名「正則列」「自己漸近列」とも呼ばれるとのこと。
日本語の方がイメージしやすいですね。

この数列はnが大きくなってもずっと飛び飛びなままなのでコーシー列ではありません。
コーシー列の定義
$\displaystyle\lim_{n,m \to \infty} \vert a_n – a_m \vert= 0$
極限をとった時に点と点の幅が0に限りなく近づいていくってことですね。
論理記号はこんなかんじ。
$\forall ε,\exists N \in \mathbb N; m,n \geq N \Rightarrow \vert a_n – a_m \vert < ε$
任意のεに対して実数の要素Nが存在し、nとm(二つ点を選ぶ)がN以上の場合$a_n – a_m$の差(点と点の幅)がε以下になる(0に近づく)。その数列はコーシー列と定義する、です。
ε – N論法が理解できていれば定義を理解するだけなら簡単ですね。
次にコーシー列の定義から性質を求めていきます。
収束する数列はコーシー列である
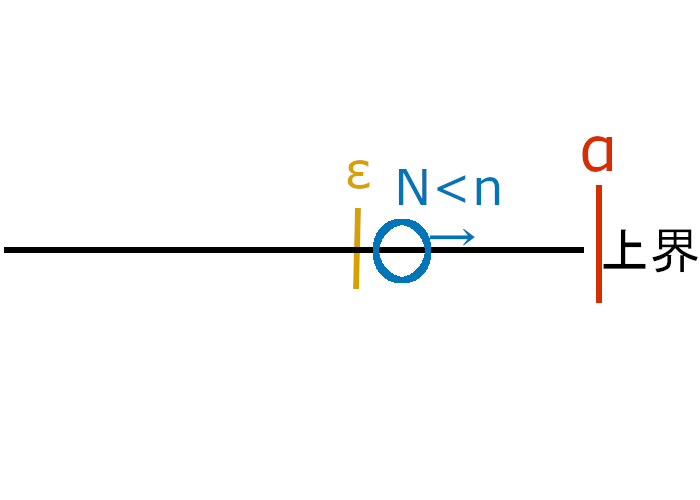
無限に続く数列がある値に頭を抑えられているのならば、当然、数列が大きくなるにつれて数と数の幅は小さく(または0に)なっていきます。
見出しの命題は直観的には自明のことなんですけどね。論理的に証明していきます。
収束する、つまり極限がどこかで抑えられること証明するために使える駒はε – N論法で、これを使ってコーシー列の定義を導きます。
とりあえず証明します。
ある数列$a_n$を考えます。
命題の通りこの数列はある値に収束するので極限をとると
$\displaystyle\lim_{n \to \infty} a_n = α$
となってαに収束します。
超小さなεを選んだとしても適切なNを選んでやれば、$n \geq N$において$\vert α – a_n \vert < ε$となることを意味します。
論理的にnより大きなmも当然、$\vert α – a_m \vert < ε$を満たすと言えます。
またコーシー列の定義$\vert a_n- a_m \vert $は収束値αの情報を加えてこんな式に変形できます。
$\vert a_n- a_m \vert = \vert a_n – α + α – a_m \vert $
表現を変えただけで論理的には同じ意味です。
上記の式は三角不等式により以下が成立します。
詳しくはリンクの補足を見てください。
$\vert a_n – α + α – a_m \vert \leq \vert a_n – α\vert + \vert α – a_m \vert $
既述の通り、右辺の二つの絶対値は極限をとるとどちらもε以下なので
$\vert a_n- a_m \vert \leq \vert a_n – α\vert + \vert α – a_m \vert < 2ε$
$\vert a_n- a_m \vert < 2ε$
となります。
εは任意の数なので2倍にしても意味は変わりません。
$ε = \frac{ε’}{2}$とやればいいので。
任意のεに対して適切なNを選べば$\vert a_n- a_m \vert$はε以下になるので、収束の定義を満たす数列は同時にコーシー列の定義を満たすことを導き出せました。

三角不等式の補足
三本の直線を幾何学的に捉えるとイメージしやすくなります。
2本の直線の長さの合計は少なくとも残りの直線の長さ「以上」にはなるだろってことです。
絶対値がある時は「幅」みたいな感じでイメージするとより分かりやすいと思います。
コーシー列は収束する
この命題は上で証明した定理の因果関係が逆転しています。
$\forall ε,\exists N \in \mathbb N; m,n \geq N \Rightarrow \vert a_n – a_m \vert < ε$
使える駒はコーシー列の定義。
この定義とこれまでに証明してきた実数の性質を使ってコーシー列が収束する(極限の定義が導き出せる)ことを示します。
ボルツァーノワイエルシュトラスの定理を利用します。
この定理は「有界数列は収束部分列を持つ」という実数の性質を表す定理です。
1.数列$a_n$が有界であること、2.収束値を持つことを証明する必要があります。
コーシー列は有界である
コーシー列の定義からコーシー列は有界であることを証明します。
$\forall ε,\exists N \in \mathbb N; m,n \geq N \Rightarrow \vert a_n – a_m \vert < ε$
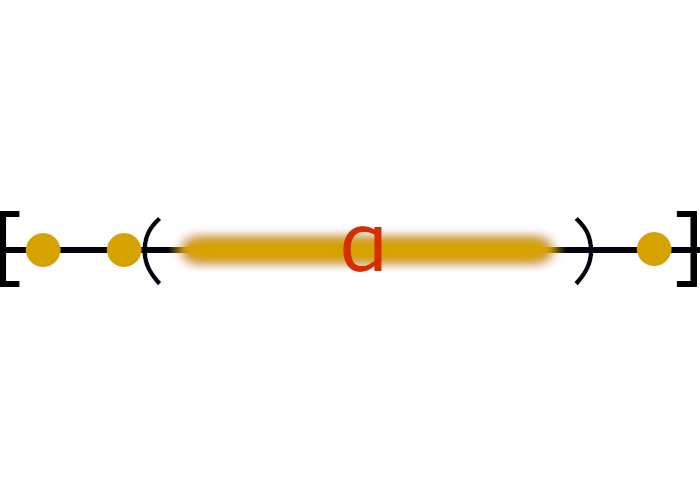
コーシー列が有界のイメージはこんな感じです。
()の中にあるぼやぼやっとしている部分はεより内側にある$n \geq N$の範囲です。
$n \geq N$の数は全部この中にあります。
●ってなっている部分は$n < N$です。
Nより小さい数は全て()の外にあります。ただ、どんなにたくさんあってもNって境目が分かるのだから、合計は有限個です。
以上が前提となるイメージです。
$n \geq N$の端っこ、上の図だと()の内側の一番小さいものか大きいもの、つまりNをmに代入します。
さらに絶対値を外してコーシー列の式を変形すると無限個要素が存在している区間が絞り込めます。
$a_N – ε < a_n< a_N + ε$
次にn < Nの部分を議論して上図の●が存在する範囲を絞り込めるかってことを確認していきます。
既述のようにコーシー列の定義より●はどんなに多く在ったとしても有限個なので、最大値と最小値が存在するはずです。
最大値の取り方が問題ですが、コーシー列の定義より$\{a_1,…a_{N-1}\}$までは必要なことは分かります。
またこれも定義より明らかですが、$a_n$は$a_N + ε$の上(下)にはないことが分かります。
最大値と最小値の取り得る範囲が絞り込めました。
$M = \max(a_1,…,a_{N-1},n_{N}+ε)$
$M’ = \min(a_1,….a_{N-1},n_{N}- ε)$
この二つで挟んでやると
$M \leq a_n \leq M’ $
となってコーシー列が有界であることが証明できます。
有界であるならボルツァーノ・ワイエルシュトラスの定理が使えます。
ボルツァーノ=ワイエルシュトラスの定理
有界な実数集合内にある数列は収束部分列を持つ。
定理より収束部分列を持つことは証明できましたが、コーシー列が収束するかどうかは証明出来ていません。
コーシー列は収束する
コーシー列が収束するかどうかを証明するまえに収束部分列について復習します。
数列の添え字が増えると同じように部分列の添え字も増えていくと部分列は定義されています。
つまり数列の極限が収束するなら部分列の極限も収束していくってことです。
部分列が収束するの定義はこれ。
$\forall ε,\exists K \in \mathbb R;k \geq K \Rightarrow \vert a_{n(k)} – α \vert < ε$
「コーシー列が収束する」ことを証明したいので、さっき証明したコーシー列は収束部分列を持つという性質とコーシー列の定義を使って極限の定義が導き出せればいいですね。
つまり、こうなるか
$\displaystyle \lim_{n \to \infty} \vert a_n – α \vert = 0$
あるいはあるK以上のkで
$\vert a_k – α \vert < ε$
こうなってほしい。
ところで話しが飛びますが、極限の式は少し変形するとこうなります。
$\vert a_n – α \vert = \vert a_n – a_{n(k)}+ a_{n(k)} – α \vert $
お馴染みの三角不等式で絶対値を外します。
$\vert a_n – α \vert \leq \vert a_n – a_{n(k)}\vert + \vert a_{n(k)} – α \vert $
上記の収束部分列の定義を見てほしいんですけど、適切なKを選ぶとそれ以上のkでは$\vert a_{n(k)} – α \vert < ε$になるって言っています。
コーシー列が収束部分列を持つことは証明しました。Kを十分に大きくすると$\vert a_{n(k)} – α \vert$は任意のεより小さくなります。
また、収束部分列と元の数列の添え字の大小関係は変化しないので$\vert a_n – a_{n(k)}\vert$の部分はコーシー列の定義の$\vert a_n – a_m \vert$の表現が変わっただけと言えます。コーシー列であるとする命題どおり、$\vert a_n – a_{n(k)}\vert$はKを極限にとばせばεより小さくなります。
$a_n – α \leq \vert a_n – a_{n(k)}\vert + \vert a_{n(k)} – α \vert < 2ε$
以上コーシー列なら同時に収束の定義を満たすので、極限をとると値αに収束することが証明できました。
極限の式から始めた方が分かりやすいような気がする。
「コーシー列なら収束する」の威力
$\forall ε,\exists N \in \mathbb N;n \leq N \Rightarrow \vert α – a_n \vert < ε$
定義通りε – N論法で収束先を確かめるなら収束先のαが分からなければなりません。
αが常に分かっているならいいですけどそんな人間に好都合なばかりではありません。
コーシー列が収束するのなら、収束先のαが分からなくても収束することだけは分かります。




コメント