微積分学の本を読み進めていたらテイラー展開ってやつが結構出てくるんですよ。
深掘りするのは億劫なんで直感でなんとなく進めていたんですけど、遂に頭がこんがらがってきてしまったので深掘りしてやってみようと決意しました。
テイラー展開の証明って簡単そうだと勝手に高を括ってたんですけどね。結構面倒くさい。
テイラー展開を論理的に納得できる程度に証明するためには、「実数の性質」から「単調増加数列の収束性」を求めて、「点列コンパクト」て概念を理解して、それで「ロルの定理」てやつをやっつけて、さらにそれで「コーシーの平均値定理」をやっつけて、そしてそれを使ってようやく「テイラー展開」をやっつけられるみたいです。
数学ってホントに深すぎ。
偉人たちの執念のバトンパスが垣間見えました。彼らの飽くなき探求心が文明を推進したと考えると足を向けて寝れませんよね。
数学勉強するのやめようかなって思ったんですけどね。
やらなきゃ気が済まないホメオスタシスが我慢してやりなさいって言うんで頑張ります。
単調増加数列の収束
「上に有界な単調増加数列には上限が存在する」って定理を証明します。
とは言っても直観的には自明である気はするんですけどね。
実数空間に部分集合Aを仮定するの?
で、そのAは上に有界なの?上限が存在するのは当たり前じゃない?って。
ところで、単調増加数列というのは
$a_n\leq a_{n+1} \leq a_{n+2}…$
といった大小関係が成り立つ数列です。
命題は「上に有界な単調増加数列$a_n$は収束する」です。
実数の性質
実数の部分集合Aが上(下)に有界な場合、Aは必ず上限(下限)を持つ。
これは公理から導き出される実数の性質です。
公理なのでとりあえずこれは疑わず上限が在るものとして話を進めます。
証明にはε-N論法を使います。
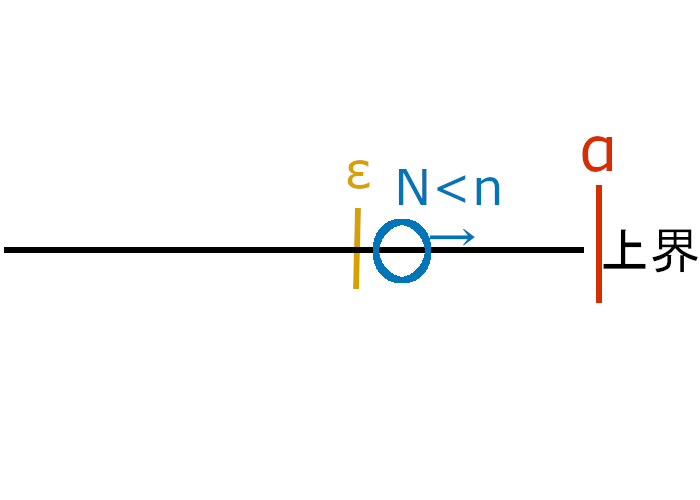
任意のε(超小さい)に対してNが存在し、$N \leq n$の範囲において$α-ε < a_n$が成り立つ(天井となる値αからεを引いた範囲に$a_n$が常に存在する)場合、実数の性質(上に有界なら~)により$a_n$は頭をα抑えつけられて上限を持ちます(極限はαに収束)。
単調増加数列の定義より$a_n \leq a_{n1} \leq a_{n2}…$と添え字が増える度に増加していきます。
これと上の実数の性質を合わせると
$\forall ε, \exists N;N \leq n \Rightarrow α – ε < a_N \leq a_n \leq α$
という不等式が成り立ちます。
論理的にはnを極限に飛ばして(どこまで増やしても)も実数の性質と単調増加数列の定義によって$a_n$は収束値αどんどん近づいて(一定の可能性もあるけど)いくんだけど、αに頭を押さえつけられてそれ以上にはなりませんよってことです。数列がその場に留まっていても、無限にちょっとづつ増加しても収束することになります。
単調増加数列の定義と実数の性質から「上に有界な単調増加数列は収束する」という命題を証明できました。
証明と言ってしまっていいのか微妙な所ですよね。
元々の意味を言い換えただけというか。



コメント