今回は対数を学びます。
最後の方に補足しますが、対数は大きな数を小さく扱うために発明されました。
具体的には航海術、天文学で利用するために開発された概念みたいです。
天文学とか航海術で扱うような大きな数同士を計算しようとすると、足し算だって面倒になりますよね。
ジョン・ネイピアは「もしも大きな数をぎゅっと圧縮する方法があって、それでいて人間が理解しやすい四則演算みたいな法則を見つけることができれば、計算処理の負担ってめちゃくちゃ軽減されるよなあ」って思いました。
僕みたいな凡人はそこで終わっちゃうんですよね。
普通はそんなことを思っても、「そうだ探し出してやろう」なんて考えませんよ。
しかしジョン・ネイピアは執念によりその方法を探し当てました。
現在は身近な例だと地震のマグニチュードとか株価の対数グラフ、星の輝きの強さみたいに、大きさの比を直感的に理解したい時などに利用されています。
星の輝きとか揺れの大きさとかって数が馬鹿でかくなってくると直感が働きにくくなって、大きさの比較が難しくなってしまいますからね。
人間の感覚も表現しやすくなります。
1000円を無くした時のショックは大人と子供で違いますよね。
全財産の内、どれだけの割合が減ったのかで人は損得勘定をするからです。
つまり、人間は価値の尺度として対数に近い感覚を持っているということです。
対数
対数は指数と対になる概念なので、まずは指数を定義しないとなんですが、それをやろうとするとどこまでも遡らないといけないのでとりあえず指数の性質は正しいと認めて話を進めます。
定義
$x = a^p$
aは底(てい)、pは指数と呼びます。
指数に関しては問題なく理解できると思うので説明はしません。
上の式はa ≠ 1,a > 0, x > 0である場合、pがただ一つに定まります。
これが指数の定義です。
底の値がマイナスの場合、1の場合、0の場合は指数の定義から外れます。
つまり$1^x$とか$0^x$、$-1^x$のようなものは指数関数とは呼びません。
こんな風に定義した理由はこの方が人間の直感的に理解しやすく都合がいいからです。
宇宙人は別の定義をしているかもしれません。
底が1なら何乗しても1のままで、底が-の場合は飛び飛びの非連続な値になってしまって使いにくいといのが具体的な理由です。
とりあえず以上が指数の定義でした。
$p = log_{ a}{ x }$
上の指数をこんな風に書き換えたものが対数です。
つまり、対数は指数ありきの概念なんですね。
外に飛び出して主役になるものが違うだけです。
aが底でxは真数と呼ばれます。
この定義から対数関数では以下の性質が求められます。
$log_{a}{a}^p = p$
左辺「aをp乗した値はaを何乗したものですか?」という質問に対しては右辺の答えは当然「p乗」となるわけです。
当たり前のことですね。
さらにもう一つ定義から導き出せるものがあります。
$a^{log_{a}{M}} = M$
左辺「$aをlog_{a}{M}$乗すると何になりますか?」という質問に対して、答えは右辺「M」。
ちょっと分かりにくいので数字に変えてみます。
$2^{log_{2}{16}} = 16$。
2を4乗すると16です。つまり$log_{2}{16}$は4。
つまり2の4乗は16と言っているだけです。
肩に乗る指数部分の表記が変わるのでややこしいですが、意味することは$2^4 = 16$です。
定義から以下が導き出せました。
$log_{a}{a}^p = p$
$a^{log_{a}{M}} = M$
定義をいじくりまわして表現の方法を変えただけなんですが、この式は対数の変換公式で重要な役割を果たします。
昔の偉人たちの苦労が垣間見えます。
僕達は教科書で結果だけ示されているので「なんでこんなことしたの?」と気持ちが悪くなりますが、昔々これが必要な状況の人がいて、執念の試行錯誤の末に何とか導き出しました。
そして、それは人類史に刻まれるほど偉大な発明でもあったわけなんです。
式の変換公式
$log_{a}{MN} = log_{a}{M} + log_{a}{N}$
どうにかこうにか定義をいじくりまわして一つの論理を構築していく、数学って面白いなあと僕が感じた要因でもあります。
対数関数の重要な公式の一つ目。
$log_{a}{MN} = log_{a}{M} + log_{a}{N}$
$log_{2}{16}$ は$log_{2}{{4 × 4}}$ に変換できて、さらに$log_{2}{4} + log_{2}{4} $みたいに変換して扱えますよってことです。
16は2*2*2*2、4乗です。2を4にするには2乗、それが二つだから2 + 2 = 4。
変換公式と一致しますね。
これは既述の定義をいじくって作った式$a^{log_{a}{M}} = M$を使うだけで簡単に導けます。
Mは$a^{log_{a}{M}}$、Nは$a^{log_{a}{N}}$なので、上記の公式の左辺に代入します。
$log_{a}{MN} = log_{a}{a^{log_{a}{M}}}a^{log_{a}{N}}$
こうなります。$MN = a^{log_{a}{M}}a^{log_{a}{N}}$なので、MとNが回りくどい表現の式に置き換わっているだけですね。
見た目以外は一切変化していません。
指数部分の表現が変わったので、その分の意味が付加されただけです。
補足
ところで、指数法則には$ a^a × a^b = a^{a+b}$という法則があります。
本当はこれを証明してからやるべきなんですけど、そうなってくると「~を証明するために…」って感じでずーっと遡って公理から全てやらなければならず、時間がかかりすぎるので何となく直観で理解できる指数まですっ飛ばして対数から始めています。悪しからず。
この指数法則の具体例だけ挙げてみると。
$5^{2 + 3} = 3125$
$5^2 × 5^3 = 3125$
同じ値になりますね。
$ a^a × a^b = a^{a+b}$が成立します。
とりあえず話を進めるためにこの法則は疑うことはせず、常に成立すると認めてしまいます。
では上記の対数の変換公式を作っていきます。
上で証明した$a^{log_{a}{M}} = M$を使います。
脱線したので話を戻すと。
$log_{a}{MN} = log_{a}{a^{log_{a}{M}}}a^{log_{a}{N}}$
MNを定義通り変換しただけ。
意味は変わってません。
次に既述した指数法則を利用し$log_{a}{MN} = log_{a}{a^{log_{a}{M}}}a^{log_{a}{N}}$を指数の足し算に変換します。
ごちゃっとしているので右辺の真数の指数部分である$a^{log_{a}{M}}a^{log_{a}{N}}$この部分に注目します。
$a^{log_{a}{M}}$と$a^{log_{a}{N}}$は指数同士の掛け算になってます。
つまり、$ a^a × a^b = a^{a+b}$の形に変形できます。
変形すると$log_{a}{a^{log_{a}{M}}}a^{log_{a}{N}} = log_{a}{a^{log_{a}{M} + log_{a}{N}}} $です。
次に$log_{a}{a}^p = p$を思い出してください。
底と真数が同じ場合、真数の肩に乗っている指数がそのまま右辺になっています。
同じように指数である${{log_{a}{M}}} + {log_{a}{N}}$がそのまま右辺に出てきます。
$log_{a}{a^{log_{a}{M} + log_{a}{N}}} = log_{a}{M} + log_{a}{N}$
よって
$log_{a}{MN} = log_{a}{M} + log_{a}{N}$
が証明できました。
「これがなんの役に立つんだよ」と思ってしまいますが、大きな数や小さな数を扱う数学では式の書き方を変えるだけで見える世界が変わってくるってことがあります。概念がとらえやすくなって扱いやすくなるからです。
手計算で大きな数を扱う昔の偉人達にはこれが必要だったんです。
次の変換公式はこれ。
$log_{a}{\frac{M}{N}} = log_{a}{M} – log_{a}{N}$
$log_{a}{\frac{M}{N}} = log_{a}{M} – log_{a}{N}$
最初のものとそっくりです。
簡単にできそうです。
定義から導き出した$a^{log_{a}{M}} = M$でMとNを変換します。
$log_{a}{\frac{M}{N}} = log_{a}{\frac{a^{log_{a}{M}}}{a^{log_{a}{N}}}}$
先ほど指数の掛け算を足し算に変換したように、指数には指数の割り算を引き算に変換できる性質があります。
その性質を利用して
$log_{a}{\frac{a^{log_{a}{M}}}{a^{log_{a}{N}}}} = log_{a}{a^{log_{a}{M} – log_{a}{N}}}$
と変換できます。
そして最後に再び$log_{a}{a}^p = p$を使って指数部分を外へ出します。
$log_{a}{a^{log_{a}{M} – log_{a}{N}}} = log_{a}{M} – log_{a}{N}$
よって
$log_{a}{\frac{M}{N}} = log_{a}{M} – log_{a}{N}$
が証明されました。
あと二つやっつけます。
$log_{a}{M}^r = rlog_{a}{M}$
$log_{a}{M}^r = rlog_{a}{M}$
$log_{a}{M}^r$は定義から導いた$a^{log_{a}{M}} = M$を使ってMを変換します。
$log_{a}{M}^r = log_{a}{a^{log_{a}{M}}}^r$
指数の変換公式$(a^m)^r = a^{mr}$を使って変換できます。
よってrがかっこの中へ入って
$log_{a}{a^{(log_{a}{M})}}^r = log_{a}{a^{(log_{a}{Mr})}}$
rと$log_{a}{M}$の掛ける順序を入れ替えてrを前へ。
$log_{a}{a^{log_{a}{Mr}}} = log_{a}{a^{rlog_{a}{M}}}$
底と真数が同じなので、$log_{a}{a}^p = p$を使うと。
$log_{a}{a^{rlog_{a}{M}}} = rlog_{a}{M}$
よって
$log_{a}{M}^r = rlog_{a}{M}$
が証明されました。
対数の式の変換公式の最後を証明します。
$log_{a}{b} = \frac{log_{c}{b}}{log_{c}{a}}$
$log_{a}{b} = \frac{log_{c}{b}}{log_{c}{a}}$
底を任意の底に変換できてしまいます。
これってめちゃくちゃ便利そうですよね。
ただこの変換公式には違和感を覚えますよね。
なので説明に入る前に、この式が醸し出す違和感について考えてみます。
こう言う直観は大切ですからね。潜在意識がこの変換公式の重要性を感じ取り、違和感という感情でもっと深く観察しろと僕に伝えてくれています。
違和感の正体は以下です。
これまでの変換公式は配役を入れ替えただけで、登場人物は変わりません。
しかしこの式はいきなり知らない奴が出てくる。映画にいきなりわけの分からん奴がでてきたような違和感。
想像力を働かせて、昔の偉人が何故この変換公式を思いついたのかを考えてみます。
多分なんですが、ある真数を任意の低に変換することで、計算処理を簡単にしたかったのだと思います。
「くそ!$log_{a}{b}$の底を任意の数cに変換できれば…この計算は一瞬で終わるのに!」って感じで。
真数のとり扱いを簡略化するためにどうしても変換したかった。
それで試行錯誤した末にたどり着いたんじゃないかと想像します。
それでは証明していきます。
定義から導いた
$a^{log_{a}{M}} = M$
を使って
$log_{c}{b} = log_{c}{a}^{log_{a}{b}}$
aの指数部分は表現が複雑になっていますが、意味としてはaに累乗してbになるものを求めています。
さらにさっき証明した
$log_{a}{M}^r = rlog_{a}{M}$
この公式を使って指数log_{a}{b}を外へ出します。
これにより変換すると
$log_{c}{b} = (log_{a}{b})(log_{c}{a})$
さらに両辺を${log_{c}{a}}$で割ると
$log_{a}{b} = \frac{log_{c}{b}}{log_{c}{a}}$
ある対数を任意の数を底とする対数で表現することができました。
好きな数に変換できることは人にとって都合がいいですよね。
人間の理解しやすい方にに変換してしまえば、直観が働くようになるので。
この変換公式が重要であることは何となく理解できます。
対数の利用
以下航海術や天文学を飛躍させた対数の威力を見てみます。
例として$2^{1000}$を挙げます。
かけ算で計算しようとすると大変ですよね。
これを対数を使って攻略します。
$\log_{10}{2^{1000}}$
2を1000乗したら?を10を何乗したら$2^{1000}$になりますか?という質問へ変えます。
この質問の答えが分かったら、10の肩にそれを乗せることで計算が簡単になりますので。
計算を進めていきます。
$log_{a}{M}^r = rlog_{a}{M}$
この変換公式を利用して上記の対数を変形します。
$1000\log_{10}{2}$
1000倍の$\log_{10}{2}$。
後は$\log_{10}{2}$を知るだけ。
$\log_{10}{2} = 0.310…$
になります。
これに1000をかけたものを10の肩に乗せれば終わりです。
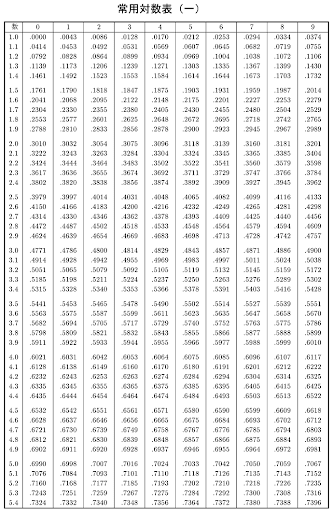
$\log_{10}{2^{1000}}$のように底を10とする対数を常用対数と言います。
人間にとって計算がしやすい底が常用として定義されました。
証明してきた変換公式を使えば、どんな形の対数でも計算処理がしやすい形に無理やり変換していけます。
また、左図の常用対数表のように対数の変換表を作りこんでおけば、計算処理をさらに簡略化できます。
昔の偉人達は夢と対数表を握りしめて大海へ挑んでいったわけです。
凄まじい執念を感じますよね。
新大陸を目指した大航海時代は今でいうAIの開発競争みたいなもんで、新大陸発見が一つの大きなロマンだったと想像できます。
現代にも残る対数表、対数尺などの道具には国家、個人が覇権を賭けて新大陸を目指していた時代の雰囲気が色濃く残されていると思います。
計算の精度が増したことで航海術が飛躍的に向上、遭難リスクが低下し死なずに済むようになりました。そうなってくると大陸間の往来が激化し、情報伝達速度が向上します。
また対数は天文学の計算負荷を低下させ「天文学者の寿命を倍に延ばした」とも言われます。天文学は地球で起こる自然現象の周期計算に利用され食料生産に貢献します。
スコットランドの数学者、ジョン・ネイピアの執念は人類文明を凄まじい力で推進することになったわけです。


コメント