素人が数学に挑戦関数列の極限

まだまだ極限の話が続きそうです。
数学は深淵です。

今回は関数列の極限についてなんですが、その前に関数列が分からないのでそこから始めます。

関数列の極限

関数列の極限

関数列

関数列
ある規則に従って順次に並べられた数または関数の列を，それぞれ数列または関数列といい，それらの列を順次に加法記号で結合した式を級数という。
コトバンク

級数
１数学で、数列の各項を順に加法記号（＋）で結んだもの。例えば、数列［a_n］で、a₁＋a₂＋a₃＋… ＋a_n＋…をいう。項が有限個であれば有限級数、無限個であれば無限級数という。
コトバンク

「『関数』の列」って意味ですね。
関数が並んだもの。

例えとして
$f_n(x) = x^n$
を挙げます。

こんな風に関数が束になったようなものが関数列です。数列が数の列なら関数列は関数の列です。

関数の極限ではnの数を限りなく増やしていくとどんな形になるのかを調査しましたが、同じようにnを増やしていくとどんな形になるかを見るのが関数列の極限です。

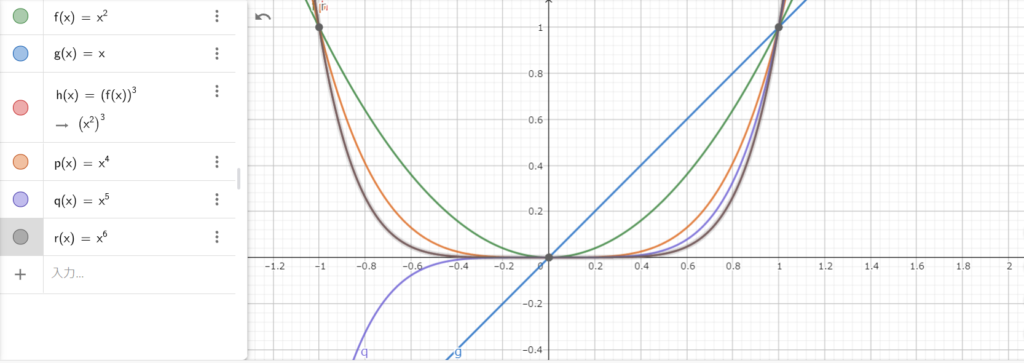
各点収束

関数列の収束には各点収束と一様収束があるみたいです。
Wikipediaの順番に従ってまずは各点収束から学びます。

{ f_n } を定義域と終域の等しい関数の列とする。（さしあたり終域は指定しないが実数と考えてもらってよい。）列 { f_n } が f に各点収束する (converge pointwise) とは、定義域のすべての点 x に対して
$\displaystyle \lim_{n \to \infty}f_n(x) = f(x)$
が成り立つことをいう。
Wikipedia

論理記号で書けば

{\displaystyle \forall x,\forall \epsilon >0,\exists N\in \mathbb {N} \ ;\ n\geqq N\Rightarrow |f_{n}(x)-f(x)|<\epsilon }

簡単に翻訳すると。
関数列$f_n(x)$の定義域内のどのxを選んでも、適切なNを選んでやればそれ以上のｎにおいては$f_n(x) – f(x)$の差（収束先の関数$f(x)$と$f_n(x)$の幅）が任意のεより小さくなる（収束していく）。
ε – N論法と論理は似ています。

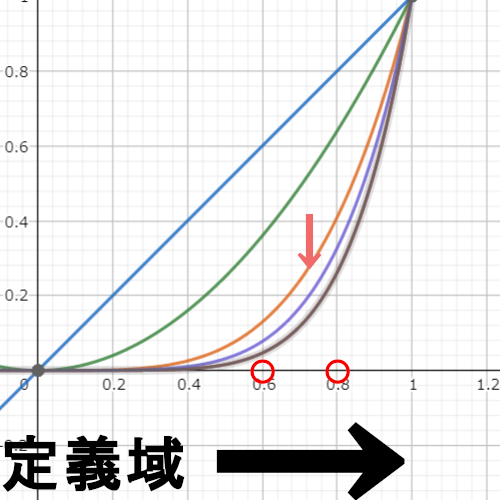
イメージはこんな感じだと思います。
定義域 0 < x < 1とすると、どのx（赤丸）を選んだとしてもnを大きくすればグラフは収束先の0へ落下していきます。

どんなにεを小さくとっても$f_n(x)$のn（べき乗）を大きくすることで$f_n(x)$と$f(x) = 0$の幅をε内に収めることができます。

関数列$f_n$は定義域0 < x 1 で極限をとるとy = 0に収束します。

着目する点（x）を決めて関数の極限を取り、その動きを見ていくので各点収束というネーミングなんだと推察できます。
まあε-δ論法よりはイメージしやすい。

これで関数列の極限は終わりかと思いきや、まだ続きます。
各点収束には問題点があるからです。
それは極限を取った時に極限を取る前の関数列の性質が失われてしまうことです。

僕は学習を始めたばかりでその問題を具体的にイメージは出来ませんが、元々の関数列の性質が失われてしまうと、元の関数列では使えた定理が使えなくなってしまうようなことが起このではないかと思います。

例えば上の$f_n(x) = x^n$の場合は極限をとると関数列の連続性が失われます。
上のグラフからも分かる通り、1は何乗しても(nをどれだけ増やしても)、y = 1です。
なので、x = 1の点ではyはピンでとめられているように動くことはありません。

定義域$0 \leq x \lt 1$の範囲では0に、x = 1では1に収束するので、極限をとると値がとびとびな不連続になってしまいます。極限を取るまでは滑らかだった$f_n(x) = x^n$の性質が失われてしまいました。

そこで登場するのが一様収束です。
関数列の性質を保存したまま極限をとれます。

一様収束

関数列 (f_n)_n∈N が極限 f: S → R に一様収束するとは、任意の ε > 0 に対し、ある自然数 N が存在して、すべての x ∈ S とすべての n ≥ N に対して |f_n(x) − f(x)| < ε が成り立つことである。
$\displaystyle \lim_{n \to \infty}\sup_{x}\vert f_n(x) – f(x) \vert < ε$
Wikipedia

論理記号で書けば
$\forall ε, \exists N \in \mathbb{N}, \forall x ; n \geq N \Rightarrow \vert f_n(x) – f(x) \vert < ε$

何故、各点収束の問題が起こったかといえば、xのある点にのみ着目して極限をとったからです。
一様収束では定義域全体がどんな動きをするのかを見ます。

それでは以下が具体的にどんなに操作になっているのかを見ていきます。
$\displaystyle \lim_{n \to \infty}\sup_{x}\vert f_n(x) – f(x) \vert < ε$

supが出てきたのでややこしいんですが、supはやりました。
最大値が数学の定義上存在しない時に最大値っぽいものをとってくる操作です。
定義域の数の中で関数列を最大化するものをｘとして極限をとった時に、$f_n(x) – f(x)$の差が任意のε（小さい数を想定）より小さくなっいる場合を一様収束と呼びます。

supの操作が分かりにくい部分ですが、$f_n(x) – f(x)$に定義域内のxを代入していって、変えてきた値の上限の値がεより小さくなる、すなわち定義域内のどのｘを選んでも、ｙが全てεに収まっているということですね。

各点収束は初めに点xを決めて、nが大きくなるとどこに収束していくかを見ていましたが、一様収束は定義域内の曲線or直線全体がnを増やすとどこに収束していくかを見ています。

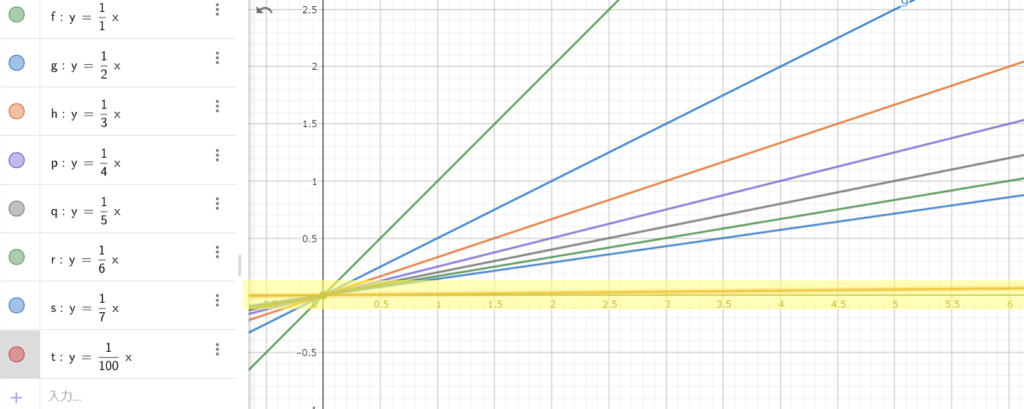
$\frac{1}{n}$のグラフです。定義域を0 < x < 5とすると、グラフから分かる通り、nを増やすと0へ向かって収束していきます。
半透明の黄色いラインがεです。$\frac{1}{100}$は定義域内のすべての値域がε内に収まっています。
εをどれだけ小さくしても、nの数を増やしていくことで対応することができます。
極限を取る前の関数列の性質が保存されるので各点収束の問題を解決しています。

今度は具体的に定義から関数列の極限を証明していきます。

$x_n$は各点収束しているか

上記の関数列$x^n$を使います。
定義域は 0 < x <1 です。
1より小さい数を同士かけると値は小さくなっていきます
0.1×0.1 = 0.01
0.9×0.9 = 0.81
かける数を増やしても小さくなります。
0.9 × 0.9 × 0.9 = 0.729
0.9 × 0.9 × 0.9 × 0.9 = 0.6561

0 < x < 1の定義域内であれば、$x^n$のnが増えれば増えるだけ0に近づいていきます。