ε – N論法は”数列”の極限をどうやって定義するのかって話でした。
ややこしい表現でしたが、理解してしまえば吐き気をもよおすようなことはなくなりました。
今度は関数の極限についてやろうと思います。
で、どんな風になっているだろうかと関数の極限についてざっと俯瞰してみたんですが、思った以上に深いなあといった感じです。
ε – δ 論法
ε(イプシロン)δ(でるた)です。
Wikipediaから引用した歴史的な背景について読んでみるとその深さが覗けます。
ニュートンとライプニッツが創設した微分積分学は、無限小(どんな正の実数よりも小さな正の数)や無限大(どんな実数よりも大きな数)といった実数の範囲では定義できない概念を用いている。このような状況はオイラーによって微分積分学が大幅な発展を遂げる18世紀まで継続された。当時の数学者達は級数の発散や収束に関する定義に無頓着なまま理論を発展させていったため、しばしば誤った結論が導かれてしまうことがあった。
Wikipedia
19世紀に入るとコーシーやベルナルト・ボルツァーノらによって、厳密な定義に基づいて微分積分学を再構築しようとする試みがなされるようになる。この時期から収束や連続に関する定義は厳密化されていく。ε-δ論法は1860年代のカール・ワイエルシュトラスの講義によって完成されたもので、これによって無限小や無限大という概念を一切使用せずに収束・連続が定義されるようになった[注釈 1][1]。数学史において、微積分学を完成させたとする評価もあるコーシーは『解析教程』(Cours d’analyse de l’Ecole royale polytechnique) で、ε-δ論法を用いて関数の連続性の定義を行った。しかし、この時点でも、連続と一様連続の区別はなかったためにコーシーは自著の中でそのことに起因する誤りをおかしている。
なお、ε-δ論法の登場により一度は数学から追放された無限小や無限大を用いる解析も現代では超実数を用いることで正当化され、超準解析(Non-standard analysis または古典的に無限小解析 Infinitesimal analysis とも呼ばれる)という分野で研究されている。
ε – δ 論法は1860年代という比較的新しい時代に一応は完成されたこと(ピタゴラスの数学教団創設が紀元前6世紀)や、無限小や無限大の概念が排除されたり取り入れられたり、と言う風に紆余曲折した歴史の成り立ちからも分かる通り、一発で理解できるような見通しのいいものではありません。
また関数の極限の分野を眺めていると連続の定義とか各点収束、一様収束の定義など扱う範囲が広いので、ちょっと大変そうな感じがしました。
とは言えまだ始まったばかり、頑張ります。
どこから始めると分かりやすいかなーと思って考えてみたんですが、関数の収束からやろうと思います。
x → a
とりあえず定義から。
高校だとxをaに限りなく近づけると、f(x)はb になる。
表記すると
$\displaystyle \lim_{x \to a}f(x) = b$
この意味の理解の前にf(x)についてです。
関数の厳密な定義についてはまだやってはいませんが、簡単に説明するとxに何か入れると、加工されて何か値が返ってくるよってことです。
f(x) = 2x
1を入れると2が、2を入れると4が返ってきます。
極限の表記は、xの値を限りなくaの値に近づけるとbが返ってくるよってことを意味しています。
補足はこの辺にしてε – δ論法の定義を見ていきます。

数列の極限のようにややこしいですね。
しかし数列の極限の定義をひたすら眺めてレベルアップしたので何となく読めるようになりました。
任意の正の実数εに対して正の実数δが存在し、適切な大きさのδを選ぶと、xからαまでの幅がδより小さくなり、またf(x)とβの差がεより小さくなるような実数xが存在する。
この時、関数の極限はβに収束する。
高校の定義通り、限りなくxをaに近づけていくとf(x)はf(a) = bに滑らかに近づいていくよってだけです。
厳密に定義するとややこしいだけ。
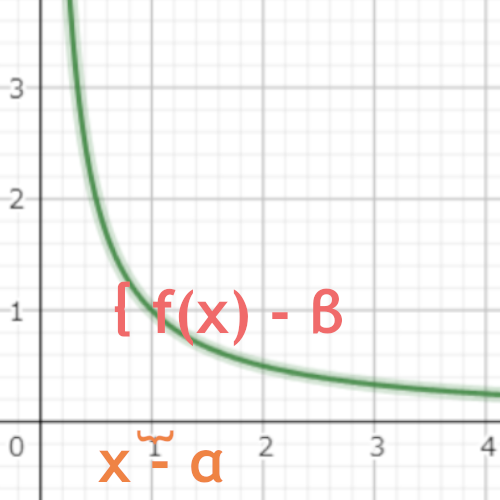
多分イメージはこんな感じ。
赤のεの幅をどれだけ小さくしても、オレンジのδの幅をそれに応じて小さくすることで、f(x)とβの差をε内に収めることができる。
高校の定義で習ったように、xを限りなく1に近づけるとf(x)の値が1に近づいていきます。
x → ∞の場合はε – N論法と同じような定義です。
$\displaystyle \lim_{x \to \infty}f(x) = β$
$\forall ε > 0, \exists L > 0;x > L \Longleftrightarrow \vert f(x) – β \vert < ε$
任意の正の実数εに対して正の実数Lが存在し、適切なLを選んだ場合、そのLより大きなxの範囲においてf(x) – βの値がεより小さくなる。
ε – N論法とほとんど同じです。
実例 $\displaystyle \lim_{x \to 1} \frac {1}{x}= 1$
実例で見てみます。

$\displaystyle \lim_{x \to 1} \frac {1}{x}= 1$
を証明してみます。
任意のε(小さいのを想定)に対して、$\vert x- 1 \vert < δ \implies \vert \frac {1}{x} – 1 \vert < ε$が成立していればいいのだから、ちょうどいいδを探してきて、それを元にε決められればよさそうなので、ちょうどいいδを探しに行きます。
まずは$\vert x- 1 \vert$がδより小さく収まる定義域(xのとれる範囲)を考えます。
定義より
1 – δ < x < 1+ δ
ですね。
グラフの{の部分です。δは小さい数を想定しているのでxがとれる範囲は「1-ちょっと」から「1+ちょっと」までです。
既述の通りεとδがそれぞれ依存するような形に持っていけたら条件を満たせるだろうって論理なので、そうなるようにεを決めようと思います。
定義域(グラフ{の幅)となる1 – δ < x < 1+ δの最大値か最小値(開区間だからおかしな表現だけど)をxの関数である$\vert \frac {1}{x} – 1 \vert$へ入力して、返ってきた値の大きな方をε(グラフ{の幅)と決めてやれば、ε=f(δ)となつのでεに対応したδが存在し、条件を満たすことが証明できます。
論理としては任意のεを決めた瞬間にδ(構造上定義域に収まる)の値がバチっと決まる関係性に持ち込めるのか?を考えようってことです。
$ \vert x- 1 \vert < δと\vert \frac {1}{ x} – 1 \vert < ε$が必然的に満たせます。
定義域の最小値と最大値を入力した値である$\vert \frac {1}{1 + δ} – 1 \vert$と$\vert \frac {1}{1 – δ} – 1 \vert$のどちらが大きいのかを知る必要があります。
どっちの幅(絶対値)が大きくなるかってことです。
比較しやすいようにに絶対値を外します。
δは正の実数なので、
$1 – \frac {1}{1 + δ} = $と$\frac {1}{1 – δ} – 1$
となります。
通分してさらにまとめると
$\frac {(1 + δ) – 1}{(1 + δ)},\frac {1 – (1 – δ)}{(1 – δ)}$
もうなんとなく大小の比較なら分かりそうなんですが、大きさの比較がしやすいように分母を揃えます。
$\frac { δ(1 – δ)}{(1 + δ)(1-δ)},\frac {δ(1 + δ)}{(1 – δ)(1+δ)} $
それぞれ計算します。
$1 – \frac {1}{1 + δ}=\frac{-δ^2 + δ}{1-δ^2}$
$\frac {1}{1 – δ} – 1 =\frac{δ^2 + δ}{1-δ^2}$
分母を揃えることで大きさが比較しやすくなりました。
δは正の実数なので計算結果より
$\frac {1}{1 – δ} – 1 > 1 – \frac {1}{1 + δ}$
となります。
ということで
$ε = \frac {1}{1 – δ} – 1$
となりεを決めるとδが決まる式が出来上がりました。
どんなεをとったとしてもその値を元にδが計算できるので条件を満たせます。
$\vert x- 1 \vert < δ \implies \vert \frac {1}{x} – 1 \vert < ε$
試しにδを求めてみます。
$ε = \frac {1}{1 – δ} – 1$
$1 + ε = \frac {1}{1 – δ}$
$\frac{ε + ε^2}{ε} = \frac {1}{1 – δ}$
$\frac{ε}{ε + ε^2} = 1 – δ$
$1 – \frac{ε}{ε + ε^2} = δ$
$δ = 1 – \frac{ε}{ε + ε^2}$
εは超小さい数を想定していますので、式の意味は「εをεともっと小さな数($ε^2$)の和で割って、出てきた1よりほんの少し小さい数からから1を引いたものがδ」です。
簡単な具体例としてεを0.01としてδを計算してみます。
$δ =1- \frac{0.01}{0.01+0.0001}$
= 1 – 0.90909090909090909090909090909091
= 0.00990099009900990099009900990099
どんなに小さなεを決めたとしてもそれに応じてδが決まりますので極限が証明できました。
補足
式変形が多く、また論理が曖昧な部分もあったんですが、とりあえず強引に押し進めたので間違っているところがあるかもしれません。
$\displaystyle \lim_{x \to 1} \frac {1}{x}= 1$
の極限を証明するだけでこんなに大変なので高校では教えなかったのかも。
骨が折れました。
論理としては、εを入力すると定義の条件を満たすδが出てくる構造が作れるなら、どんなεを選んでも定義の条件をみたせるよねってことです。
この論理あってるかな。
間違っていたら教えてください。
実例 $\displaystyle \lim_{x \to 1} \frac { (2x^2 – x -1)}{x – 1}= 3$
今度は見出しの関数の極限をε – δ論法で確認していくわけですが、その前に極限という概念が必要な理由を簡単におさらいします。
極限は数学で定義できない領域をほんの少しでも覗くための概念だと理解しています。
例えば$\frac{1}{0}$は数学では定義できません。
しかし$\frac{1}{0.0000000001}$は定義できるので、0で割るは定義はできないんだけど、限りなく大きな数になるんじゃないかなーってことは分かります。
0の数を増やしていけば∞に大きくなることがなんとなくイメージできるからです。
また物理学などで重要となる微分の定義はこうなっています。
$f(x)′= \displaystyle \lim_{a \to 0}\frac { f(x + a) – f(x)}{a}$
力学は”その瞬間の速度”を求めたい時がありますが、速度の概念の定義上、厳密にそれを求めることができません。
なので「限りなくその瞬間に近い速度」を求めることができる極限の概念が必要になります。
閑話休題。
見出しの関数の極限が定義できるのか見ていきます。
その前に何故こんな関数を選んだのかです。
この関数はこんなグラフをしています。
一見すると一直線ですが…
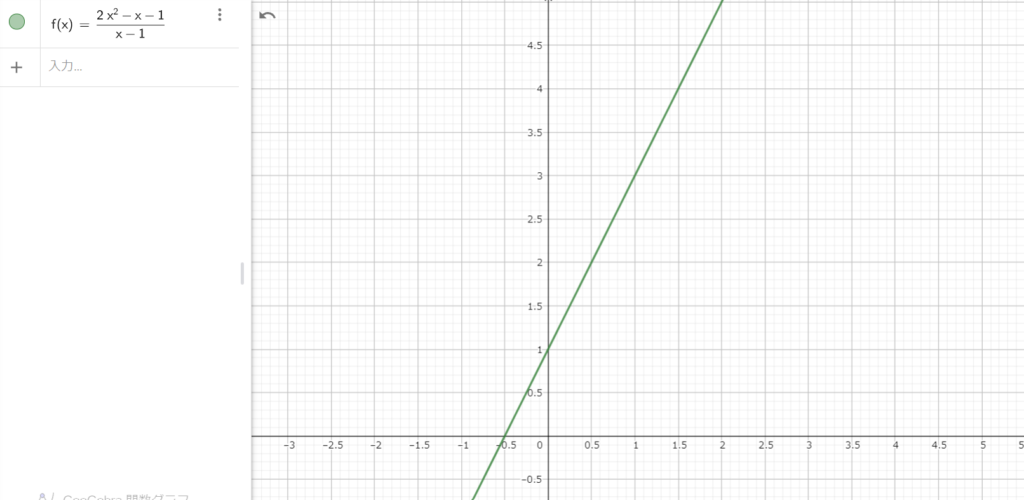
座標(1,3)にどんどん近づけていきます。
すると
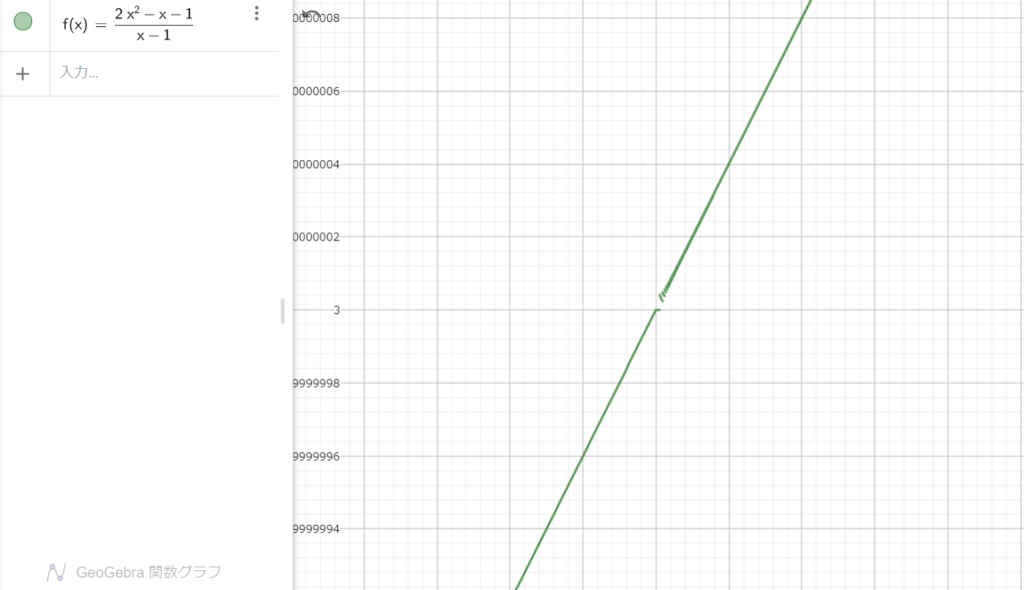
ぽっかり穴が開いています。
この関数はx = 1を定義できないんです。
そんな時に極限が利用できます。
限りなくx = 1に近い値は求めることができますからね。
$\displaystyle \lim_{x \to 1} \frac { (2x^2 – x -1)}{x – 1}= 3$
それではこの関数の極限をε – δ論法で証明していきます。
任意のεとそれに対応するδを考えます。
既述のようにεとδは依存関係にあってほしい(εを決めた時に自動的にδが決まると嬉しい)ので、
まずは定義域を絞り込みます。
定義の条件から
$\vert x – 1 \vert < δ$
この絶対値を外して1を移項。
1 – δ< x < 1 + δ
「1-ちょっと」か「1+ちょっと」に収まっていれば$\vert x – 1 \vert < δ$を満たせます。
また、この定義域の最大値と最小値(ニュアンスでお願いします)の値をf(x)に入力して、どちらか大きい方をεとすれば$\vert \frac {1}{x} – 1 \vert < ε$が満たせます。
そしてこの関係が作れることを証明できれば極限を定義できます。
これだと分かりにくいので、因数分解して形を整えます。
$\frac { (2x^2 – x -1)}{x – 1} = \frac{(2x + 1)(x – 1)}{x – 1}$
分母分子の(x -1)がキャンセルされて
2x + 1
δは正の実数だからxに代入すると返ってくる値が大きくなるのは1 + δ
$\vert 2(1 + δ) + 1 – 3 \vert = 2δ$
2δをεとおいて
$\vert \frac { (2x^2 – x -1)}{x – 1} – 3 \vert < ε = 2δ$
$δ = \frac{ε}{2}$
εの大きさはδに依存してているのでεを決めると必然的にδも決めることができます。
この関係を証明できたので極限が定義できます。
試しにε=0.1とおくと
δ = 0.05となります。
x = 1で3に収束することは分かりました。
補足
論理的には正しい気はしますが、どこか見落としている疑いが捨てきれません。
数学を勉強すると自らの論理性の乏しさを痛感しますね。
実例 $\displaystyle \lim_{x \to 1} \frac {2}{x – 1}= 極限なし$
この関数はxへの近づき方によって正の無限大や負の無限大に発散の仕方が変わりますので、極限はありません。
グラフを見るとx = 1付近で正負の両方へ発散しているのが分かります。
つまりx = 1では定義ができません。

さっきx = 1で極限を取った$\frac{1}{x}$もx = 0では極限なしです。

一旦ここで終わっておきます。
一応やってはみたもののまだまだしっくりこない。
微分までやるとスカッとするのだろうか。
余談
普通、グラフ見たら「近づいてんじゃん」って思うんですよ。
でも、「ちょっと待って、本当に近づいているか分からないぜ?証明してみよう」って言い出した狂人がいたんです。
実際に見に行くことはできませんで、論理によって確かめようと思ったってことです。
コーシー(Augustin Louis Cauchy)って人です。
この人がいたからこそ、微分て分野が進歩したらしいんです。
ホントに何もかも、疑ってかかるのって大切ですよね。


コメント