 暇つぶしに見て
暇つぶしに見て 素人が数学に挑戦 上限と下限
関数列の極限を扱うときに出てきた概念なので学習します。 定義 急ぎ足でざっと行きます。 上界と下界 $\forall x \in A$について$x \leq a$の時、aはAの上界でAは上に有界であるという。(集合Aの中の一番大きな数をとっ...
 暇つぶしに見て
暇つぶしに見て  よもやま話
よもやま話  プライベート
プライベート  トレーニング
トレーニング  戦略
戦略  未分類
未分類  暇つぶしに見て
暇つぶしに見て  選手分析
選手分析  トレーニング
トレーニング 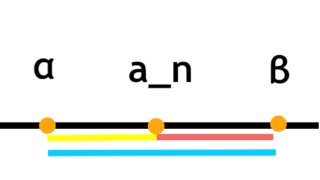 暇つぶしに見て
暇つぶしに見て  技術
技術  技術
技術