引用WIIS

引用wiis

有理数の大小関係

加法の大小関係 デデキント切断の準備をします。 感覚的には「任意の正数xに任意の正数y足した値はxより大きくなる」は自加法律を見れば自明です。ただ、年の為に確認します。 0<1,x(仮定) 0+x<1+x(加法律) x<1+x(単位元) 0...

riku-nagahama.xyz

2025.04.25

無理性の証明

有理数はℤ/ℕで表される数。

偶数は約分できるので、有理数は分母か分子のいずれかが奇数になります※1。

例)2/4=1/2,3/6=1/2
分母分子は互いに素

x²=2となるようなxを求めます。そのような有理数があると仮定すると
(p/q)²=2
p²=2q²
となります。

pを奇数と仮定
(2n+1)²(仮定)
4n²+2n+1(x²の定理)
2(2n²+n)+1(分配法則)①
pが奇数ならその平方は奇数であり、かつ任意の奇数の平方は奇数であることが示せました。
例)1×1=1,3×3=9,5×5=25

実数は偶数と奇数に二分でき、奇数かつ偶数は矛盾します。
2q²は自然数の二倍なので偶数です。
すなわち、pを奇数とすると等式p²(奇数)=2q²(偶数)が矛盾するので、背理法によりp=¬奇数=偶数が示されます。

①よりpを偶数であると仮定します。
p²=2q²※1(有理数定義)
(2n)²=2q²(①)
4n²=2q²(平方)
2n²=q²(有理数同値関係)②
自然数nのn²の2 倍と同値になるのでq²は偶数です。

①と有理数の性質※1より、qは奇数でなければならず、また、この場合は既述のようにその平方は奇数となります。従ってqの平方は奇数です。
これは平方が偶数であることを示す②と矛盾します。
前提である「qが奇数である」は誤りであることが示されました。背理法によりqは偶数です。

以上の証明をまとめると。
pは偶数である、かつqは偶数である。が成り立ちます。
これは大前提である「有理数は分母分子の何れかが奇数である」と矛盾します。
背理法により「有理数ではない=無理数である」が導かれますます。
従って
x²=2を満たすxは無理数であることが証明されました。

0.9999999999... = 1の論理　世にも奇妙な数学の世界

秩序を作ると無秩序が排出される 極限の概念を学んできて、ε - N論法、ε - δ論法などの「極限」を定義する論理はなんとか理解できたんですが、限りなく1に近づいた0.99999...は本当に1なの？ってことが置き去りだったなって感じました...

riku-nagahama.xyz

2021.10.26

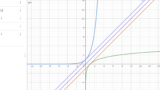
素人が数学に挑戦　金利計算中に現れた不思議な定数、ネイピア数

e= 2.71828 18284 59045 23536 02874 71352 …ネイピア数はこんな定数です。円周率と同じく無理数。 ネイピア数はヤコブ・ベルヌーイが複利計算をしている最中に発見しました。銀行に金を預けると預けた額に数％付...

riku-nagahama.xyz

2021.11.01

素数が無限にある証明を背理法で

論理的に正しいと定義される推論の形式の続き「背理法」を見ていきます。 背理法 定義 【背理法】とは、ある命題Pを証明したいときに、Pが偽であることを仮定して、そこから矛盾を導くことによって、Pが偽であるという仮定が誤り、つまりPは真であると...

riku-nagahama.xyz

2023.03.10

矛盾と否定の認識

恒偽式は矛盾とも呼ばれ、恒真式の対義語です。 矛盾と否定 矛盾 恒真式（こうしんしき、トートロジー、英: tautology、ギリシャ語のταυτο「同じ」に由来）とは論理学の用語で、「aならば aである (a → a) 」「aである、また...

riku-nagahama.xyz

2023.04.13

背理法などの議論の枠組み

恒真式恒真式（こうしんしき、トートロジー、英: tautology、ギリシャ語のταυτο「同じ」に由来）とは論理学の用語で、「aならば aである (a → a) 」「aである、または、aでない (a ∨ ￢a)」のように、そこに含まれる命...

riku-nagahama.xyz

2024.04.16