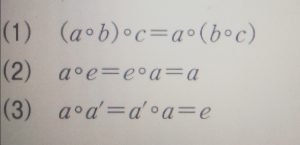
群

同型写像

群演算の一意性

X:群
X∈x,x⁻¹,y

x･x⁻¹=x･y
x⁻¹･x･x⁻¹=x⁻¹･x･y
e･x⁻¹=e･y
x⁻¹=y

xの逆元と異なる要素yを群から取ってきてxに作用させた場合に結果が同じ。

群の同型写像の集合Mを定義。その中から要素を取り出して合成。

g⊗h(x)=g(x)･h(x)
と定義①。
i(g･h(x))
こんな関数だと思ってください。

g⊗h(e)(仮定)
g(e)･h(e)(定義①)
e･e(群)
e
同型写像を合成した送り先で単位元の性質は保存されます。

g⊗h(x･y)
g(x･y)･h(x･y)
g(x)･h(x)･h(x)･h(y)
g(x)･g(x)･h(y)･h(y)
g(x)･h(x)･g(y)･h(y)
g⊗h(x)･g⊗h(y)

演算して送ったものと、送ってから演算したものが同じ。結合法則。

g⊗h(e･e⁻¹)
g⊗h(e)･g⊗h(e⁻¹)
g(e )･h(e⁻¹)･g(e)･h(e ⁻¹)
g(e )･g(e⁻¹)･h(e)･h(e ⁻¹)
e･e⁻¹･e･e⁻¹
e･e
e

単位元と逆元の法則が保存される。(準)同型写像を送った群を(準)同型写像で送る行為を繰り返しても群の性質は保たれる。逆元の保存。

aをa’へ送る準同型写像fがあれば、a’をaへ送る準同型写像f⁻¹も定義できる。

演算が保存されていれば群は同型。