数学ってほんとに切りがない。
実数の性質を勉強していて気が付いたらベクトル空間って概念に広がっていって、それをさらに深めると線形代数って学問が出現しました。
行列ってやつが出てきたので学びます。
ざっと見た感じベクトル空間と似たようなものでした。
高校で聞いたことある程度なので学びなおします。
行列
定義
行列はベクトルと同じように表記します。
横の並びを「行」縦の並びを「列」と呼びます。
$\begin{pmatrix}a & b \\ c & d \end{pmatrix}$
この例だと「行」はa,bとc,dで「列」はa,cとb,dです。
$ \mathbb a = \begin{pmatrix}a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn}\end{pmatrix} = [a_{ij}]m×n_{(1\leq i\leq m,1\leq j\leq n)}$
m×n行列の表記法。
全部行列を意味しています。
行列式を書き表すのって面倒ですからね。簡略化した右辺のような記法も用意されています。
ちなみにコードで行列式を書き表すとこんな感じ。
コード
\mathbb a = \\begin{pmatrix}a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn}\end{pmatrix} = [a_{ij}]m×n_{(1\leq i\leq m,1\leq j\leq n)}
これをいちいち打ち込むの面倒です。既に嫌気がさしているので表記法が途中で変わるかもしれません。
行列の加法
次に加法を見ていきます。
といってもベクトルの加法と手続きは同じ。
行列aとbを考えます。
$\mathbb a = \begin{pmatrix}a_{11} & a_{12}\\ a_{21}&a_{22} \end{pmatrix},\mathbb b = \begin{pmatrix}b_{11} & b_{12}\\ b_{21}&b_{22} \end{pmatrix}$
$\mathbb a+ \mathbb b = \begin{pmatrix}a_{11} + b_{11}& a_{12} + b_{12}\\ a_{21} + b_{21}&a_{22} + b_{22} \end{pmatrix}$
分かりやすく実例を上げます。
$\mathbb a = \begin{pmatrix}1 &2\\ 3&4 \end{pmatrix},\mathbb b = \begin{pmatrix}5 & 6\\ 7&8 \end{pmatrix}$
$\mathbb a+ \mathbb b = \begin{pmatrix}6 & 8 \\ 10 &12 \end{pmatrix}$
同じ成分同士を足し合わせます。
同じ大きさの行列のみ足し算ができます。
行列の乗法
スカラー倍(実数)の場合はベクトルのスカラー乗法と同じ。
$\mathbb a = \begin{pmatrix}a_{11} & a_{12}\\ a_{21}&a_{22} \end{pmatrix},b = b $
$\mathbb ab = \begin{pmatrix}ba_{11}& ba_{12}\\ ba_{21}&ba_{22} \end{pmatrix}$
各成分をスカラー倍するだけです。
具体例でみると
$\mathbb a = \begin{pmatrix}1 & 2\\ 3&4 \end{pmatrix},b = 5 $
$\mathbb ab = \begin{pmatrix}5 & 10\\ 15&20 \end{pmatrix}$
行列同士の積
行列同士の積は行列と実数をかけるスカラー乗法と違った計算規則が定義されています。
ちょっとだけ複雑です。
$\mathbb a = \begin{pmatrix}a_{11} & a_{12} & a_{13}\\ a_{21}& a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{pmatrix},\mathbb b = \begin{pmatrix}b_{11} & b_{12} &b_{13}\\ b_{21}&b_{22}&b_{23} \\ b_{31} & b_{32} & b_{33} \end{pmatrix}$
$\mathbb{ab} = \begin{pmatrix}a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31}& a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32} & a_{11}b_{31} + a_{12}b_{32} + a_{13}b_{33}\\ a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31}& a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32} & a_{21}b_{31} + a_{22}b_{32} + a_{23}b_{33} \\ a_{31}b_{11} + a_{32}b_{21} + a_{33}b_{31}& a_{31}b_{32} + a_{32}b_{22} + a_{33}b_{32} & a_{31}b_{31} + a_{32}b_{32} + a_{33}b_{33} \end{pmatrix}$
簡単な規則性ですが、ちょっと混乱します。
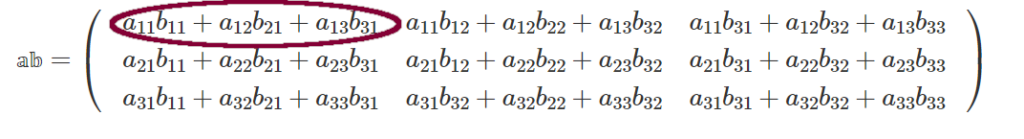

赤丸の部分は左図の規則で作られています。
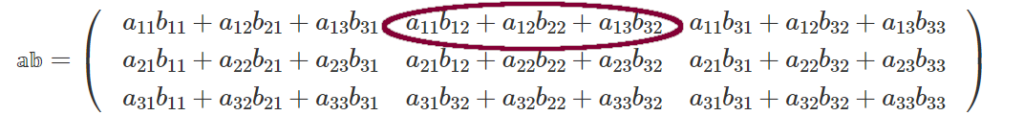

ちょっと面倒ですが、規則は簡単です。
後に命題として証明していきますが、行列積の大切な部分は交換法則ab = baが成り立たないことです。
また同じ列の大きさが同じものでなければ計算できません。
3行なら3行、4行なら4行としか乗算ができません。
行列の演算の定義は分かったとして、なぜこのように定義されているかの理解が大切ですよね。
加法とスカラー乗法に関してはベクトル空間の記事で、「実数の演算のように振舞ってほしいから」だ解説しました。
ただ、行列同士の積に関しては初めて見ると意味不明です。
ちょっと深堀してその理由について考えていきます。

コメント