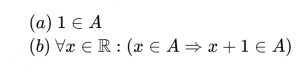
帰納的集合引用WIIS

加法律引用WIIS
数の大きさ
∀y,∀x∈ℝ,∀n∈ℕy<nx
自然数は帰納的集合なので上に有界ではない、かつ実数は加法律によりどこまでも大きくできます。
∀x,y>0,∃n∈ℕ:y<nx
自然数に上界がないこと、実数に下界(無限小)と上界(無限大)がないことを簡潔に表すと上のような形になるのかなと。
順序群Gにおける正の元x, y について、xがyに対して無限小である(あるいは、yがxに対して無限大である)とは、任意の自然数 n について nx がyより小さいこと、つまり以下の不等式が成立することである。
x+⋯+xn<y.
順序群Gにおける正の元の対x, yで、xがyに対して無限小になっているようなものは存在しないときGはアルキメデス的であると言われる。
アルキメデスの性質は体系の中にの無限小と無限大が現れないことの要請(性質?)。
a<a+1(帰納的集合)
x+0=x<x+1(加法律)
数の順序の性質の言い換え。
また、
x<y<z⇒z⁻¹<y⁻¹<x⁻¹
の定理を用いれば任意の小さ実数εよりも小さな有理数は常に創れます。
つまり、任意の小さなεをとってきて、その乗法逆元をとっても、それより大きなnはいくらでも存在することが保証されます。
従って、
ε⁻¹<n(仮定)
n⁻¹<(ε⁻¹)⁻¹(乗法逆元の定理)
n⁻¹<ε(逆元の逆元)
自然数の乗法逆元は有理数の定義を満たします。すなわち、任意の小さなεよりも小さい有理数は常に存在します。
無理数+無理数
無理数+有理数=無理数(有理数性質)
有理数=無理数-無理数(加法逆元)
π-3=x(仮定)
-3=π+x(加法逆元)
有理数+無理数=無理数、となりますが、無理数+無理数=有理数となる可能性があります。
整数と無理数
任意の有理数の間には無理数が存在することは既に証明しています。
x<y<z⇒z⁻¹<y⁻¹<x⁻¹
「実数をいくらでも大きくできる」は、上の性質を利用すれば「実数はいくらでも小さくできる」と言い換えられますす。
任意の無理数に大きな有理数を選んでその乗法逆元をかければ0に近い無理数εを創れます。
有理数+無理数=無理数です。仮に差の小さな任意の有理数x<yを選んでも、x<x+ε<yの関係を創れます。すなわち任意の有理数の間には必ず無理数を創れます。
負の数と正の数で無理数が挟めるのかも確認します。自明に見えますが念の為。x,yを有理数、aを無理数とします。
有理数xより小さな無理数を任意に選びますを
0<a<x(仮定)
-x<a-x<0(加法律)
-x<a-x<0<a(推移律)
-x<a(推移律)
-x<a<x(≤推移律)
正負の数で無理数は挟めます。
これまでで分かったことをまとめると。
1.任意の整数の間には必ず有理数がある
2.任意の有理数の間には必ず無理数がある
差の小さな無理数a<bを選んだとしてもそれを有理数x<yで挟みこんでその差を縮小していけば
x<a<x+y/2<b<y
とa,bを分割できますから、論理的には、任意の無理数の間に有理数を創ることができると言っていいはず…
結論。数直線はギチギチに詰められている。
https://riku-nagahama.xyz/2025/06/24/アルキメデスの性質その三/









コメント