乗法の自然数の閉性

暇つぶしに見て

2025.05.10

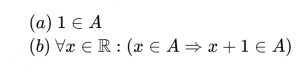
引用WIIS

任意の乗法を自然数へ送る集合が帰納的集合である証明。

A={y∈ℕ,x∈ℝΙx・y∈ℕ}①
yを1と仮定すると
x･1∈ℕ(乗法単位元)
単位元は任意の自然数を自然数へ送るので、Aは1を含みます。

定義を満たすy=aを選びます。
x ･a∈ℕ(①)
また、前回自然数の加法が閉じていること、すなわちa+1∈Aは既に証明しましたのでax+xは自然数に属します。
従って
ax+x(加法閉性)
x･(a+1)(分配法則)
と変形できます。

Aは帰納的集合の定義を満たすので
x･y∈ℕ⊂A
となります。

除法は閉じていない

任意の自然数xは帰納的集合の定理より0<x①。

自然数に乗法逆元があると仮定して矛盾を導きます。

まずは自然数乗法の順序の性質の確認。x<y⇒z･x<z･yの証明。

2x(仮定)
(1+1)x(自然数大小関係)
x+x(分配法則)
2x=x+x(仮定②)
x<x+x(加法律)
1･x<2･x(②)

同様の論理により、x<y⇒x･z<y･zとなります。

正の1<xの実数同士の乗法は順序関係を保存します。

乗法逆元が自然数に存在すると仮定して矛盾を導きます。

1<x⁻¹(仮定)
x<x･x ⁻¹(乗法律)
x<1(乗法逆元)

自然数の性質1<xと矛盾します。
よって自然数は分数を持ちません。