ド・モルガンの法則
ふと、自然演繹て、少しも”自然”じゃないよな、と感じるようになってきました。頭の中で遊ぶ分には面白いのですが。形式的に考え過ぎることがヒトの自然な思考から精神を引き剥がし、無味乾燥で無意味なことをしていると感じる時があります。
今の僕のように感じた人達の勢力が直観主義という立場でしょう。気持ちは分かります。無矛盾律や背理法からの導出は、やや乱暴さを感じます。
日本語と文化の影響なのかな。
数学の哲学において、直観主義(ちょっかんしゅぎ、英: Intuitionism)とは、数学の基礎を数学者の直観におく立場のことを指す。
数学的概念とは数学者の精神の産物であり、その存在はその構成によって示されるべきだという立場から、無限集合において背理法によって非存在の矛盾から存在を示す証明を認めなかった。それゆえ、無限集合において「排中律」、すなわちある命題は真であるか偽であるかのどちらかであるという推論法則を捨てるべきだと主張し、ヒルベルトとの間に有名な論争を引き起こした。 ヒルベルトの形式主義は、直接的にはブラウワーからの批判的主張に対し排中律を守り、数学の無矛盾性を示すためのものと考えることができる[1]。
ド・モルガンの法則を形式的にやると下のようになります。多分。正直に言うと、人の直感に反しているようで気持ちが悪い。そんな風に推論する人はいないたまろうと。
[A](仮定)
A∨B(∨導入)
¬(A∨B)(仮定)
⊥(排中律)
¬A(背理法)
[B](仮定)
A∨B(∨導入)
¬(A∨B)(仮定)
⊥(排中律)
¬B(背理法)
¬A∧¬B(∧導入)
¬(A∨B)→¬A∧¬B(→導入)
[A∧B](仮定)
[¬A](仮定)
A(∧除去)
⊥(排中律)
¬A→⊥(→導入)
[¬B](仮定)
B(∧除去)
⊥(排中律)
¬B →⊥(→導入)
[¬A ∨¬B](仮定)
⊥(∨除去)
¬(A∧B)(背理法)
¬A∨¬B →¬(A∧B )(→導入)
¬A∧¬B(仮定)
[A](仮定)
¬A(∧除去)
⊥(排中律)
A→⊥(→導入)
[B] (仮定)
¬B(∧除去)
⊥(排中律)
B→⊥(→導入)
[A∨B](仮定)
⊥(∨除去)
¬(A∨B)(⊥除去)
¬A∧¬B→¬(A∨B)(→導入
下の方がむしろ”自然に”感じます
(A∪B)^c
(A^c∩B^c)
(A∪B)^c⊂(A^c∩B^c)
口語に直すと「『AまたはB』ではない状態。つまり、Aだけであることはあるし、Bだけであることもある。ただし、その両方であることはあり得ない。よって、Aであり、かつBでは」
形式的には論理が飛躍にしたように見えてしますが、僕の感覚的には自然てます。
(A^c∩B^c)
x∉A∧x∉B
x∉(A∨B)
(A∨B)^c
二行目から三行目の変換が強引な感じ否めないので補足。
「Aではい、かつBではない」という主張は、「AまたはBではない」という主張に変換できるような気がします。
ブラウワーは、数学的概念とは数学者の精神の産物であり、その存在はその構成によって示されるべきだという立場から、無限集合において背理法によって非存在の矛盾から存在を示す証明を認めなかった。それゆえ、無限集合において「排中律」、すなわちある命題は真であるか偽であるかのどちらかであるという推論法則を捨てるべきだと主張し、ヒルベルトとの間に有名な論争を引き起こした。
ブラウワーは「AであるかAでないかが分からない場合もある」を説明する例として、「円周率の無限小数の中に0が100個続く部分があるかどうか分からない」というものをあげていた。
ある学会でブラウワーがこの話をしたとき、「しかし神なら100個続く部分があるかどうか分かるのでは?」という質問を受けたが、ブラウワーはそれに対し「残念ながら我々は神と交信する方法を知りません」と答えた。
直観主義の文脈ったこれかなと。僕は真と偽の2値だけで説明する排中律は、ヒト的というか原始的というか、何が引っかかるものがあります。つたり、2値のいずれかに決論が収束するって形式によっては説明不要な現実があるんじゃないの?と。数学は現実を説明しようとしてない、と言う人もいるだしょうが。
いずれにしても本気で議論していた数学者もいるようで安心しました。ブラウワーほど厳密には考えられないにしても、彼の言わんとしている感情はなんとなく理解できます。





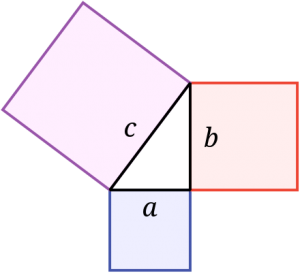
ピタゴラスの定理
上の書籍の面積や堆積の問題を解こうとして躓きましたので、中学の復習。幾何学ってなんだろうと感じますよね。
三角形とはと。図形としてならイメージできますが、その細部を削ぎ落として抽象化した場合の三角形とは。
ぱっと思いつく範囲だと正三角形は、「任意の3点の関係を表した何かを全て集めた集合の内にある、ヒトが「それが唯一の関係だ」と感じられる何か。」とかですかね。
緩和休題。
a²+b²=c²
現在の日本では三平方の定理()とも呼ばれている。戦前の日本では勾股弦の定理()と呼ばれていた。「ピタゴラス」と冠しているが、発見を含めて、定理と何か関係があるのかから知られていない。
書籍の問題はこんな感じ。
長さ21m、幅16mの長方形の屋根の上の中央に、高さ8mの旗竿を立てる。
ワイヤーを用意し、その一方を屋根の四隅に固定する。そのもう一方を旗竿の頂点に結ぶ。そして、その四本のワイヤーの張力で旗竿を直立させる。
ワイヤーの合計の長さはいくつか。
屋根の短い辺を横、長い辺を縦と呼び、屋根のある点をAとするなら、旗竿を立てる屋根の中央の位置はAから8m横へ、10.5m縦へ移動した地点。すなわち、ピタゴラスの定理よりAから旗竿を立てる中央までの長さは√横²+縦²。
x=√10.5²+8²=√110.25+ 64=√174.25=13.200…m
底辺と高さが分かっているので再びピタゴラスの定理により√13.2²+8²=√283.24…=15.435025105259=15.430…m
合同
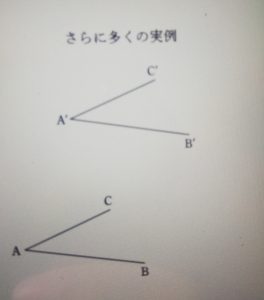
∠ABC=∠A’B’C’が等しいことの証明。
まずは我流平行の定義。直観的に、
AB∥CDだとするなら、∠ABC
ならば
次の問題。
別の平面に存在する平行線が形成する角が等しい証明。
AC∥A’C’
AB∥A’B’
ならば
△ABC≡△A’B’C’
の証明。
角を形成する直線ACとA’C’の上に、AD=A’D’となるような点DとD’を置き、AD=A’D’を作ります。
またADからABへ垂直に戦争を引きます。
平行の性質より、∠C=∠C両端の角は等しくなります。よって
△ABC≡△A’B’C’
合同な図形の性質より
∠A=∠A’
幾何学も面白そうだと感じます。
実数乗法の一意性

x×y=x×z⇒y=z
xにかけた後の結果が同じならyとzは同じであってほしい。そうならないなら、上の定義は現実の運用には耐えられません。
x×y=x×z(前提)
y(仮定)
y×1(乗法2)
y×(x×x⁻¹)(乗法3)
(y×x)×x⁻¹(乗法1)
(x×y)×x⁻¹(乗法4)
(x×z)×x⁻¹(前提)
(z×x)×x⁻¹(乗法4)
z×(x×x⁻¹)(乗法1)
z×1(乗法3)
z=y
実数の乗法には一意性があります。
x⁻¹×(x⁻¹)⁻¹=1(乗法3)
(x⁻¹)⁻¹×x⁻¹=1(乗法4)
(x⁻¹)⁻¹×=x(乗法一意性)
乗法逆元の逆元は元々の元。
x=0∨y=0⇒x×y=0(0の乗法)
¬(x×y=0)⇒¬(x=0∨y=0)(対偶)
x×y≠0⇒(x≠0∧y≠0)
関連記事



コメント