可付番集合可算集合とは N と濃度が等しい集合のことである。すなわち、集合 S が可算であるとは、自然数全体の集合 N との間に全単射が存在することをいうウィキペディア自然数との全単射性が認められる集合が可付番。偶数は可付番偶数2...

濃度の件で、そう言えば代数的数なるものがあったなと。果たしてその濃度はどれほどか証明しよう、と思い立ったのですが、『そもそも「代数的数」を知らん』と気が付きました。

深掘りしたら「群」という概念と遭遇。
情報の大部分が捨像されたような定義だと感じられ、恐らくはそれが代数的数の根にあるだろうと。

数学における群（ぐん、英: group）とは、ある二項演算とその対象となる集合とを合わせて見たときに結合性を伴い単位元と逆元を備えるものをいう。

集合 G とその上の二項演算 μ: G × G → G の組 (G, μ) が群であるとは、以下の3つの条件を満たすことをいう：

（結合法則）任意の G の元 g, h, k に対して、μ(g, μ(h, k)) = μ(μ(g, h), k) を満たす：

$(\forallg,h,k\inG)[μ(g,μ(h,k))=μ(μ(g,h),k)].$

（単位元の存在）μ(g, e) = μ(e, g) = g を G のどんな元 g に対しても満たすような G の元 e が存在する：

$(\existse\inG)(\forallg\inG)[μ(g,e)=μ(e,g)=g].$

このような e は存在すれば一意であり、G の単位元という。

（逆元の存在）G のどんな元 g に対しても、μ(g, x) = μ(x, g) = e となるような G の元 x が存在する：

$(\forallg\inG)(\existsx\inG)[μ(g,x)=μ(x,g)=e].$

このような x は存在すれば一意であり、この x を g の G における逆元といい、しばしば g⁻¹, あるいは演算を加法的に書く場合には −g で表される。

ウィキペディア

群、その心は

整数と実数の加法と乗法の規則を抽出した概念になっていると思います。

0を含まない自然数の加法には単位元と逆元はありせん。0を含めても逆元がありません。乗法には逆元がありません。従って自然数は群ではありません。

引用の1は、関数を作用させる順序によってその結果が変わらないことの要請。
例えば整数の加法。
(a+b)+c=a+(b+c)
定義を満たします。

2は任意の要素に対して何もしない要素の存在を要請しています。
a+0=0+a=a
整数は定義を満たします。

3ある要素に作用させると単位元となる要素、すなわち加法なら、作用させて0にできる要素の存在の要請。
a+(-a)=(-a)+a=0
整数は定義をみたします。

以上の123を満たすことから整数の加法は郡です。乗法も群です。
整数の加法と乗法を抽象化して定義しておけば、これが適用できる範囲なら全て群として扱えます。

{a,f()}
だけの集合であっても、上の取り決めをすれば群として扱えます。

f(a)=a

1.結合則
f(f(a),a)=f(a,f(a))=(a,a)
2.単位元
f(a)=a
3.マイナス元
f(a)=a

単純な定義なので、整数や実数のような有用なものであるのかは置いておいて、簡単に郡は作り出せます。

関数の集合Aから任意の三つの要素を取り出して合成し任意の元を代入する場合も
f×g×h(x)=((f×g)×h)(x)=(f×(g×h))(x)

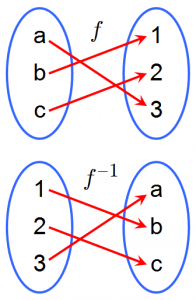
In mathematics, the invers function of a function $f$ (also called the inverse of $f$ ) is a function that undoes the operation of $f$ . The inverse of $f$ exists if and only if $f$ is bijective, and if it exists, is denoted by $f^{-1}.$

For a function $f:X\toY$ , its inverse $f-1:Y\toX$ admits an explicit description: it sends each element $y\inY$ to the unique element $x\inX$ such that $f (x) = y$ .

ウィキペディア

単射の場合は逆関数も存在するとのこと。

認識の細部を捨像し、最低限必要不可欠な前提だけに絞り込んでいるので、その応用範囲はかなり広い。

結合法則とは何か

群に要請される規則は三つだけ。それだけで話を完結させているのは面白いなと。

結合法則は、「数える順番によってはその結果は変化しないでほしい」という願いで、左から数えたり右から数えたりすると総数が変わる、とか、見る角度を変えると映画の内容が変わる、右から引いたり左から引いたりすると流さの変わる直線、なんてことがないことの要請だと思います。

ヒトが観測できる現実空間においては、当たり前と言えば当たり前の要請です。

数学、とくに抽象代数学におけるアーベル群（アーベルぐん、英: abelian group^{[注釈 1]}）または可換群（かかんぐん、英: commutative group）は、群演算が可換な群、すなわちどの二つの元の積も掛ける順番に依らず定まる群を言う。名称は、ノルウェーの数学者ニールス・アーベルに因む

ウィキペディア

数学における環（かん、英: ring）とは、台集合に「加法」（和）および「乗法」（積）と呼ばれる二種類の二項演算を備えた代数系のことである。

ウィキペディア

抽象代数学における環上の加群（かぐん、英: module）とは、ベクトル空間を一般化した概念で、係数（スカラー）を体の元とする代わりに、より一般の環の元としたものである。つまり、加群とは（ベクトル空間がそうであるように）加法的なアーベル群であって、その元と環の元との間に乗法が定義され、その乗法が結合的かつ加法に関して分配的となるようなものである。

ウィキペディア

係数
一次式の係数環 A とその上の加群 E が与えられたとき、E の元を表す一次式 ∑ a_n x_n (a_n ∈ A, x_n ∈ E) を考えることができる。a_nたちはこの一次式の係数と呼ばれる。

ウィキペディア

抽象代数学において可換体（かかんたい、仏: corps commutatif）あるいは単に体（たい、英: field）^{[注 1]}とは、零でない可換可除環、あるいは同じことだが非零元全体が乗法の下で可換群をなすような環のことである。そのようなものとして体は、適当なアーベル群の公理と分配則を満たすような加法、減法、乗法、除法の概念を備えた代数的構造である。

ウィキペディア

数学において代数的構造（だいすうてきこうぞう、algebraic structure）とは、集合に定まっている算法（演算ともいう）や作用によって決まる構造のことである。

代数的構造を持つ集合は代数系（だいすうけい、algebraic system）であるといわれる。

具体的なさまざまな代数系から、それらが共通してもつ原理的な性質を抽出して抽象化・公理化したものが、代数的構造と呼ばれるのである。

ウィキペディア