「論理包含」で正気を失う

暇つぶしに見て

2023.01.082023.03.30

部分集合から集合の相等関係の法則を導く証明の際に使用した下の法則を理解するために論理包含を学びます。

【ドモルガンの法則】
$\displaystyle (P\rightarrow Q)\land (Q\rightarrow P)\rightarrow (P\Leftrightarrow Q)$
集合の相等関係

「PならばQ」「QならばP」ならばP＝Q。
当たり前のように感じますけどね。
ただそれは日常の感覚。それが数学へ応用できるかは公理から証明する必要があります。

論理包含

論理包含

命題

上のような式の変形の関係は論理包含と呼ばれ、推論の構造を抽象化して一般化したものです。

論理包含（ろんりほうがん、含意（がんい）、内含、英: implication、IMP）は、第1命題が偽または第2命題が真のときに真となる論理演算である。条件文（じょうけんぶん、英: conditional）とほぼ同じものである。
Wikipedia

「AならばBは真or偽」。
$P \rightarrow Q$
と表します。
もう少し意味を掘り下げると「『前提P（命題1）』が真かつ『結論Q（命題2）』が真の場合、P→Qは真を出力する演算となります。
下の表の法則になっています

[table id=implication /]

分かりやすく例で考えます。
前提「1+1である」結論「2である」となった場合の構文全体の真偽を見ます。
・「1+1である（真）」ならば「2である（真）」である、は真。
・「1+1である（真）」ならば「2ではない（偽）」である、は偽。
・「1+1でない（偽）」ならば「2である（真）」である、は真
・「1+1でない（偽）」ならば「2ではない（偽）」である、は真

「ちょっと待て」となりますよね。
上から二つは受け入れたして、下の二つは受け入れがたい。

Wikipediaにはこうあります。

【例】
P が偽ならば、Q の真偽にかかわらず「P ならば Q」が真である (en:Vacuous truth)、という定義は直感的に受け入れ難く、しばしば哲学的な議論の主題となる。

【日常的な例】
ある人が「この仕事が失敗したら辞表を出す」と言ったとしよう。この言葉が嘘となるのは、仕事が失敗したにもかかわらず辞表を出さなかった場合のみである。仕事が失敗して辞表を出したならば約束を守ったのであるし、仕事が成功して（失敗せず）かつ辞表を出さなかったならば、やはりその人は嘘を言わなかったことになる。仕事が成功したにもかかわらず（何か他の理由で）辞表を出した場合も、やはり嘘を言ったとはみなされないであろう。すなわち、先の宣言では仕事が成功した場合のことは何も言っていないのであるから、辞表を出そうが出すまいが本人の自由である。
Wikipedia

上の例で言えば「1+1」以外の話はしてないよってことです。
「1+1」という前提が真なら「2」以外はあり得ません。
しかし、下から二つ目は前提がないので「2+0」でも「4÷2」でもいいし、「2+3」でも「1+2」でもわけです。最後に関してはなんでもありです。
数学や論理学が始まった頃は「ならば」は日常的な意味で使われていたが、数学的な思想の元で概念が洗練されるに従い、日常的な意味から乖離してきた、とWikipediaにはあります。

論理包含は集合を元にした演算

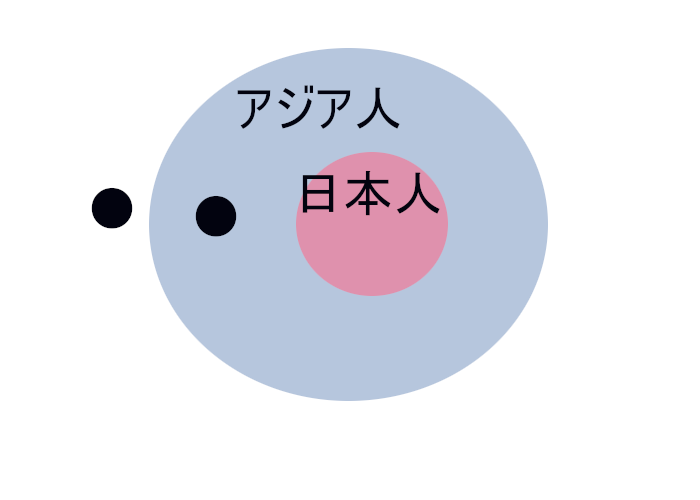
少し分かりやすく「『日本人である』ならば『アジア人である』」を例に考えてみます。

・「『日本人である』ならば『アジア人である』」は真
日本人はアジア人の部分集合、●は日本人の誰か（元）。
・「『日本人である』ならば『アジア人である』でない」は偽
アジア人の外に日本人の集合はありませんので、偽だと分かります。

問題はここから。
・「『日本人である』ではないならば『アジア人である』」は真
確かにフィリピンとかタイの可能性もあるけど、この前提ならヨーロッパ人かもしれない、アメリカ人も認めなければならない….だけど真。

・「『日本人である』でないならば『アジア人である』でない」は真。
これはまあ、分かる気がしないでもない。
日本人ではないからといって、アジア人であるとは言えない。ヨーロッパ人かもしれない。

前提が偽なら構文全体は真って謎ルールじゃないですか。
そう感じるのは僕だけ？一般的な感性からかけ離れているような。
一般的な感性とはことなる、数学の元となる思想が何かあると思います。

謎ルールを考察

写像は集合Aの元が集合Bの元をただ一つを指し示す規則でした。
様々な原因が同じ結果を指すことはあっても、原因が定まった場合、結果は一つしかありません。
「原因には結果と道筋がありますよね」を厳密化した概念って感じです。
これをヒントに考えます。

【写像】
集合 A の各元に対してそれぞれ集合 B の元をただひとつずつ指定するような規則 f が与えられているとき、f を「定義域（あるいは始域） A から終域B への写像」といい

$\displaystyle f \colon A \to B,\quad A{\stackrel {f}{{}\to {}}}B$
などと表す。
Wikipedia

考えをまとめる為に直感したままを書き出していきます。

数学は前提から結論を導く証明を行います。
それは前提と結論の一対一対応を作ること。
前提を決めたのなら結果との完全な一対一対応でなければならない、ただし、結果を満たす前提は複数あってもいい。
ある方法では証明できなくても別の方法で証明できればいいわけです。
つまり、構文全体が真っていうのは結論を導くまでの証明手続きの確かさのことを言っているのでは？てことですね。

・「1+1でない（偽）」ならば「2である（真）」である、は真
一旦前提と結論は無視します。
「1+1ではない」って前提なら「2+0」を結果を求める証明の仮定として引っ張り出してもいいわけで、そうだった場合の証明方法は間違っていません。

・「1+1でない（偽）」ならば「2ではない（偽）」である、は真
「0=0」「1+2＝3」などを好きな前提とその証明を採用することが認められているので、無限の前提と結論を想定することで真は創り出せます。
「1+1でないなら2でなくてもいいだろ」って証明は確かです。

前提と結論の因果関係というよりは、構文として成立するかってことなんだと納得しました。

公理的にそれが認められているのかってことを探すと寿命が来てしまいそうな予感がしますので、とりあえずこんな感じの自分なりに考えで納得して前へ進みます。