直和の定義の次は直積を見ていきます。
忘れないようにメモしておきますが、これは整数の定義を理解したいというのが発端となっています。
直積
概要
数学において、集合のデカルト積(デカルトせき、英: Cartesian product)または直積(ちょくせき、英: direct product)、直積集合、または単に積(せき、英: product)、積集合は、集合の集まり(集合族)に対して各集合から一つずつ元をとりだして組にしたもの(元の族)を元として持つ新たな集合である。
Wikipedia
具体的に二つの集合 A, B に対し、それらの直積とはそれらの任意の元 a ∈ A, b ∈ B の順序対 (a, b) 全てからなる集合をいう[1]。集合の組立記法(英語版) では
$A × B = \{(a,b)| a \in A \land b \in B\}$
と書くことができる。有限個の集合の直積 A1×⋯×An も同様の n-組からなる集合として定義されるが、二つの集合の直積を入れ子 (nested) にして、(A1 × ⋯ × An−1)× An と帰納的に定めることもできる。
順序対
順序のついていない単なる対(つい)に対応して用いられる数学用語。 二つの元a、bに対してaとbのみからなる集合{a, b}をaとbの対とよぶ。
コトバンク
数学における順序対(じゅんじょつい、英: ordered pair)は、一口に言えば対象を「対」にしたものである。二つの対象 a, b の順序対をふつうは (a, b) で表す。ここで、「順序」対において対象の現れる順番は重要であることに注意しなければならない、すなわち a = b でない限り (a, b) という対と (b, a) という対とが相異なる[
Wikipedia
集合は非順序対です。
従って{a,b} = {b,a}、{a,a} = {a}となります。順序は関係ないからです。
順序対は(a,b) ≠ (b,a)といった感じで順序に意味を持たせます。
Wikipediaによれば色んな定義があるようですが、その中で最も有名なのがクラトフスキー式。
クラトフスキーは順序対をこう定義しました。
集合a,bを組み合わせて作った集合(a,b)を
$(a,b) :=\{\{a\},\{a,b\}\}$
例えば順序を入れ替えてみると
$(b,a) = \{\{b\},\{a,b\}\}$
従って
$ \{\{a\},\{a,b\}\} ≠ \{\{b\},\{a,b\}\} $
このように順序対の定義が順序の交換を封じています。
※:=は右辺で左辺を定義しますの意
a = bだった場合は
$(a,b) = \{\{a\},\{a,b\}\} = \{\{a\},\{b\}\} = \{\{a\}\}$
となるので以下の論理で順序の意味が無くなっちゃう感じかなあと。
$\{1,1,1,1,1\} = \{1\} = 1$
順序対でも集合の元が全て同値だった場合、それは論理的に非順序対になります。
()は順序対を表し、{}は非順序対の集合を表す記号です。
思い返せば義務教育の座標も()で表しました。順序対だからですね。
補足
上の説明よりこっちの説明の方がいいなと感じたので別の証明を載せます。
$(a,b) :=\{\{a\},\{a,b\}\}$
この定義に当てはめて以下を考えてみます。
$(a,b) = (c,d)$
$\{\{a\},\{a,b\}\} = \{\{c\},\{c,d\}\} $
集合の数の対応から
$\{a\} = \{c\}$
$\{a\} ≠ \{c,b\}$
であることが分かりますので
$\{a\} = \{c\}$
$\{a,b\} = \{c,d\}$
従って
$(a,b) = (c,d)$
順序対の定義が上の形をしている理由が証明できました。
論理積
直積の定義式にある論理記号の$\land$は論理積を表していて、論理積はAND演算です。
高校の何かの授業でやった気がするので高校の授業を真面目に聞いていた人は知っているかも。
コンピューターの電気回路図でも出てくるので見慣れた感じはあります。
数理論理学において論理積(ろんりせき、英: logical conjunction)とは、与えられた複数の命題のいずれもが例外なく真であることを示す論理演算である。
Wikipedia
与えられた命題が二つあった場合、その二つが真だった場合論理積演算は真を返し、どちらかが偽だった場合は偽を返します。
両方が偽だった場合も偽。
このシンプルな演算が論理積です。
余談ですが、コンピューターはこの論理積と論理和を複雑に組み合わせて高度な演算処理を行っています。
スマホ、パソコン、あらゆるものに利用されています。
現実世界における数学の威力って半端じゃないですよね。
閑話休題。
以上を踏まえると以下の直積の論理積は
$A × B = \{(a,b)| a \in A \land b \in B\}$
「直積集合A×Bの元は集合A,Bの元の順序対の組み合わせで構成されているよ」です。

左の A × B の青い枠の中身の組み合わせが集合A,Bの直積集合の元になります。
シンプルでイメージは掴みやすい。
例
やりながら気が付きましたが、前回直和の例に挙げた座標の例は少し間違えていますね。
直積の定義を学んでたら
「順序対じゃないなら直和に向きはなくね?」
って
定義も直和は集合を定義していて、直積は順序の組み合わせを定義しています。
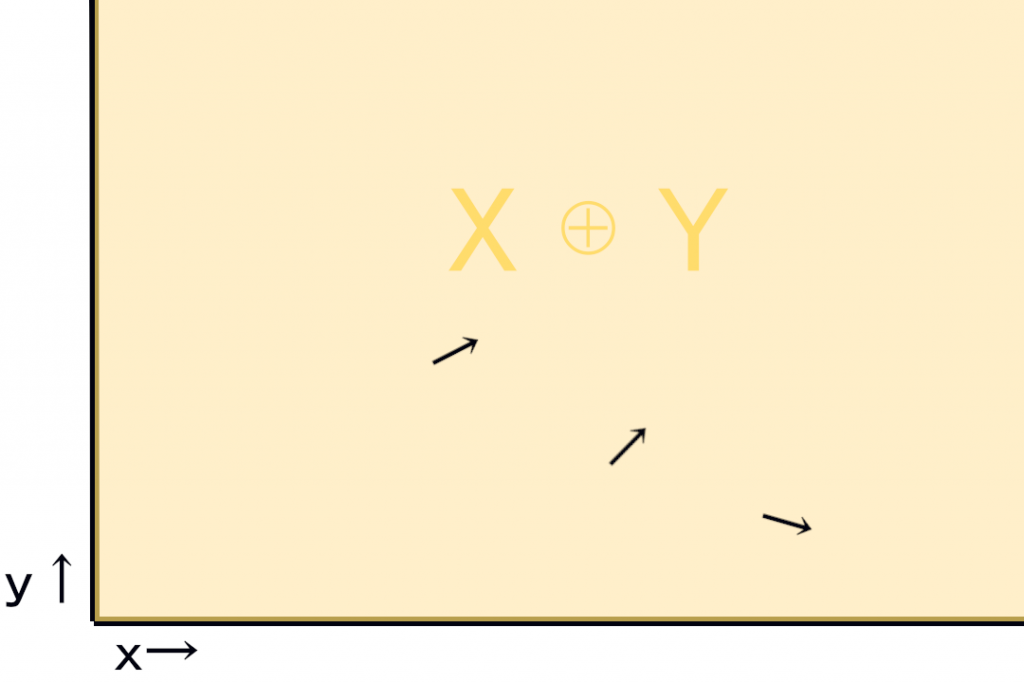
黄色の平面が直和で矢印が直積って感じですかね。
まだ断言する自信はない曖昧な理解なので間違えてたら更新します。

コメント