以下の記事で関数列の極限についてはやりました。
一応は理解できたんですが、知識は整理されるとその先の細部が散らかっていきますよね。
で、疑問が浮かびました。
一様収束ではsup操作を行いますが、この時定義域内の数で$f_n(x)$を最大化するものはどうやって見つけてくるのか、です。
可能な組み合わせの数が膨大になってくると総当たり方式も通用しなくなっていきます。
小さな規模ならなんとなく直観で論理を構築できるけど、直観が働かないほどの規模になってくるとそうもいかない。日常でもよくある話です。
直観が働かない領域はどうすんの
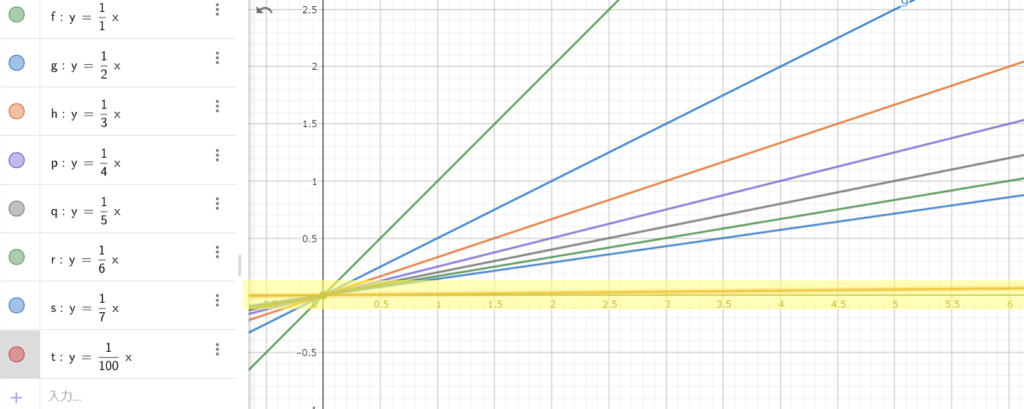
$f_n(x) = \frac{1}{n}x$のグラフです。
このグラフは直観的に0に収束しそうだってことは分かります。
また、$\frac{1}{n}$は式の形からnを極限に飛ばしたら0に限りなく近くなることも想像できます。
しかし、複雑な形の関数列になると、その収束先を予測することは難しくなると思います。
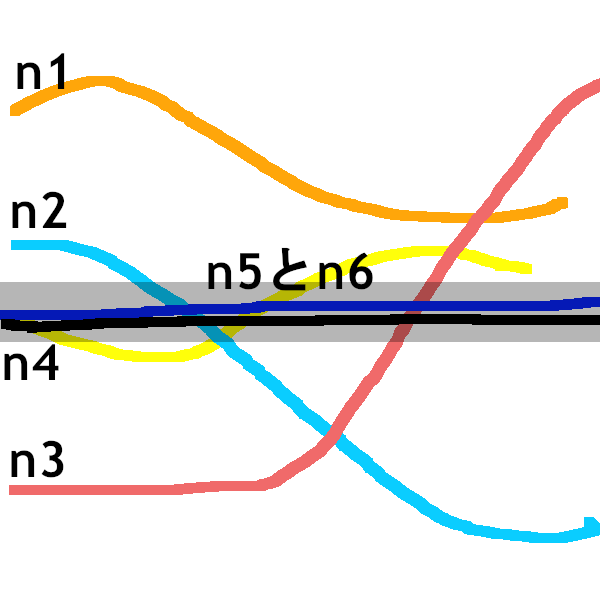
雑な図ですが、こんな動きをする関数列があると仮定します。
n5,n6以上から黒の半透明のライン(ε)に収束するんですが、それ以下のnではその様子は全くありません。
こんな風に動きが予測できないような関数列の場合、どこに収束するかの直観が働きません。
また、この図に映っていない範囲でn5,n6の値はεを超えているかもしれない、とも思えます。
挙動が予測できないような関数列で定義域が大きくなる場合っていちいち総当たりで計算してられないんで、論理的に命題を導いていくと思うんですが、それはどんな風になるだろう、つまり直感で予測できない場合の論理の組み上げ方を知りたいということですね。
収束や極限の定義の理解が甘いだけなのかもしれませんが、この疑問が頭に浮かんだのでもう少し考えを深めていこうと思います。
微分したら最大値が分かる
色々調べてみて気がつきましたが、微分ですね。
微分は曲線の点の傾きを調べる操作です。最大値は傾きが0になります。

最大値の傾きは0になるので、微分して0になる定義域内のxを探せばいいことになります。
いちいち計算するのでなく、論理的に最大値が求まるのって気持ちがいい。
例題
教員試験の問題を引用して極限の命題を解いていきます。
命題は関数$f(x) = nx(1 -x )^n 定義域(0 \leq x \leq 1)$は一様収束する。
この関数列を極限へ飛ばすと一様収束するか、を確かめていきます。
関数の形を見ると1より小さな数(定義域より)をn乗し、それをnx倍する形になっています。
1より小さい数は累乗すると0に近づいていきます。nxの部分もnに1より小さい数をかける形になっていますので、nが大きくなればなるほど0へ近づいていくことになります。
つまり、nを極限へ飛ばすと0と0のかけ算になることが論理的に導き出せて収束先が0であることが分かります。
関数列の極限の定義通り求めていきます。
既述の通り収束先は0なので$f_n(x)$の上限だけ考えればいいことになります。
$\displaystyle \sup_{0 \leq x \leq 1} \vert f_n(x) – 0 \vert = \displaystyle\sup_{0 \leq x \leq 1} \vert f_n(x) \vert$
定義域は閉区間なので上限は最大値maxと同じ。
最大値を求める方法は既述の微分です。
微分の定義はまだやっていませんが、とりあえず微分で最大値が求まると認めて処理を進めていきます。
積の微分をした後の式はこうなります。
$f(x)’ = n(1-x)^n+{n^2}x(1-x)^{n-1} = n(1-x)^{n-1}\{(1-x)+nx\}$
補足
上の式を無理やり変形して
$n(1-x)^n = n(1-x)^{n-1}(1-x)$
共通項をまとめています。
ちょっと曲芸的な変形ですけど、論理的には同義です。
微分の傾きが0になるところが最大値で、その時のxを求めたいので
$f(x)’ = n(1-x)^{n-1}\{(1-x)-nx\} = 0$
こうなります。
かけて0になるのはどちらかが0、どちらも0の時です。
どちらにもxが含まれていますが、簡単そうなのは右側。
$1-x+nx = 0$
$1 = x + nx$
左辺をxでくくると
$1 = x(1 + n)$
xの式にしたいので(1+x)で両辺を割って
$x = \frac {1}{1+n}$
1をn+1で割っているので定義域内にも収まっています。
最大値を求めるxが分かりました。
これを代入して
$\displaystyle \sup_{0 \leq x \leq 1}\vert f_n(x) – 0 \vert= \frac{n}{n + 1}(1 – \frac{1}{n + 1} )^n $
nを極限へ飛ばします。
$\frac{n}{n + 1}$は極限を取ると1となるので省略できます。
1よりほんの少し小さい数を無限大乗する$(1 – \frac{1}{n + 1} )^n$はネイピア数の定義です。
$\displaystyle \lim_{0 \to \infty} (1 – \frac{1}{n + 1} )^n = \frac{1}{e}$
ネイピア数が定数だと言うことは、$f(x) = nx(1 -x )^n$は定義域の最大値をとったときに0へ収束しないと言えるので、一様収束しません。
命題は偽。
ネイピア数は対数の分野で登場する不思議な定数です。
極限が一通り終わったので今度やります。


コメント