 数学とか
数学とか 頭の体操七
逆元の逆元 -(-x)は逆元の逆元という意味。裏の裏は表、の証明。 公理主義実数論の公理から。 ∀x,∃-x∈ℝ:x+(-x)=0 任意の元xを選ぶとその逆元は必ず存在します。 (-x)+(-(-x))=0(R3) -(-x)+(-x)=0...
 数学とか
数学とか  数学とか
数学とか  数学とか
数学とか  数学とか
数学とか  数学とか
数学とか 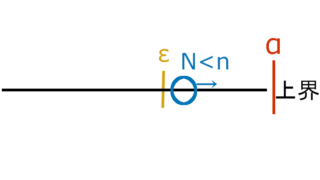 数学とか
数学とか