自然数の加法の閉性

暇つぶしに見て

2025.05.09

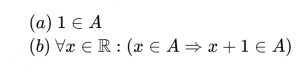
帰納的集合引用WIIS

帰納的集合

定義は単純です。
帰納的集合は、1を持ち、かつ1と任意の元の加法が閉じていること。

具体的には実数、正の実数、非負の実数、0を含む自然数、0を含まない自然数、正の整数、正の有理数などですかね。

自然数

公理主義では帰納的集合の共通部分を自然と定義しています。
従ってこの場合は
minℕ=1
となります。

順序
正と負の乗法は負かつ
0<x(仮定)
0<x･x⁻¹(乗法律)
0<1(乗法逆元)
なので、1は0より大きくなります。

実数の加法律より
0<0+1<0+1+1<0+1+1+1<…
と順序が定義できます。

乗法律

加法の閉性
A={∀x,y∈ℕ⇒x+y∈ℕ}①

上の式を満たす集合があると仮定します。
任意のx∈ℕをℕへ送るy∈Y⊂ℝ②を考えます。

ある自然数xに実数yを作用させると、その結果は自然数に送られる(演算の閉性)と仮定する。この場合の実数yにはどんな性質があるのか(帰納的集合の性質は満たすのか)を考える。

x∈ℕ(仮定)
y=1(仮定)
(x+1)∈ℕ(帰納的集合または①)
1は集合Aに含まれます。

また、yをaとけば
x+a∈ℕ(①)
①より、結果は自然数へ送られます。

また、自然数は帰納的集合なので、
(x+a)+1∈ℕ(帰納的集合)
と変形できます。
さらに、
(x+a)+1=x+(a+1)∈ℕ(結合法則)
と変形すれば
(a+1)∈A
が演繹できます。

Aは帰納的集合の要請を満たします。

自然数は帰納的集合の部分集合。すなわち
ℕ⊂A
となるので、任意の自然数の加法は閉じていると証明されました。

加法律

1-2∉ℕの証明

負数は
-1+1=0
となり帰納的集合の要請を満たしません①。

x<y(仮定)
x-y<y-y(加法律)
x-y<0(加法逆元)
x-y∉ℕ(①)