線形変換
行列とか線形性とか線形写像はかなり難しく感じる、やってもやってもやってもきりがない。
学問だから当たり前だけど深いわ。
これまでの人生には現れてこなかった、現れても認識できなかった概念だからだと思いますが、理解するのも時間がかかるし、理解してもその先が見えないから「で?」ってなります….
写像
行列はあるベクトルをあるベクトルへ変換する写像(関数)でした。
写像は集合の要素から集合の要素を選ぶための規則で、もっと分かりやすく言うと$f(x) = y$の式で表せる関数でした。
xに何かを入れるとyに変換されるのが関数です。
行列も写像で、ベクトルに作用しそれを別のベクトルへ変換します。
今回は行列が線形変換(写像)であるなら、この概念をどこまで広げていけるのかを見ていきます。
ただ、この前の続きで行列によるベクトルの線形変換の例から先に見ていきます。
線形変換の例
線形変換は別名「線形写像」。
ある集合をある集合へ変換する規則、つまり基底ベクトルを別の基底ベクトルへ変換することで空間全体を歪めて、ベクトルの集合全体の形を変えてしまうものです。多分。
反転
前回の復習。
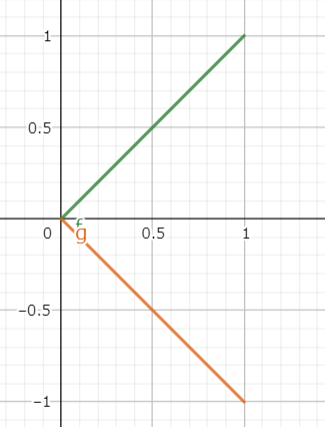
行列$\begin{pmatrix}1 & 0\\0 & -1 \end{pmatrix}$は基底ベクトルに作用して空間をx軸で対照に反転させるものです。
緑がfオレンジがgです。
$f = \begin{pmatrix}1 \\ 1 \end{pmatrix}$
$g = \begin{pmatrix}1 & 0\\0 & -1 \end{pmatrix}\begin{pmatrix}1 \\ 1 \end{pmatrix} = \begin{pmatrix}1 \\ -1 \end{pmatrix}$
緑のベクトルをx軸で線対照に反転させる行列です。
別の例を見ていきます。

ベクトルu = ベクトルb
です。
作る時に間違えました。
ベクトルa,bが基底ベクトル$a = \begin{pmatrix}0 \\ 1 \end{pmatrix},b = \begin{pmatrix}1 \\ 0 \end{pmatrix}$です。
それらに行列$f = \begin{pmatrix}2 & 2 \\ 2 & -2 \end{pmatrix}$を作用させると。
$\begin{pmatrix}2 & 2 \\ 2 & -2 \end{pmatrix}\begin{pmatrix}b \\ a \end{pmatrix} = \begin{pmatrix}2b + 2a \\ 2b +(- 2a)\end{pmatrix} = \begin{pmatrix}c \\ d\end{pmatrix}$
基底ベクトルに作用させて空間を変形させるのがベクトル。
今の理解だとこんな感じ。

行列の一列目は変換後のベクトルがx軸のどこに移動するのか、二列目はy軸がどこへ移動するのかを示しています。
ベクトルをどの座標へ飛ばすのかが分かりやすくなるので直感的にベクトルの変換がイメージしやすくなりました。
二次元を記述する基底ベクトルは二つ。
で、それをx軸側に2スカラー倍してバーンと飛ばす。
y軸方向には2と-2スカラー倍飛ばす。
基底ベクトルが変換されるから空間がその分だけ伸び縮みする。
少しづつですが複雑に見えた行列積の規則の全体像が見えてきました。
ベクトルの変換規則が行列積です。
僕は勝手に実生活における世界観で行列を理解しようとしていましたが、それが良くなかった。
日常生活で築き上げた(天才は線形性が見えるかも)世界観の更新が必要ですね。
日常生活レベルの観念で行列積を捉えようとするから理解不能になる。
世界観が違う。
実際には同じ世界を見ているんだろうけど、その抽象度が段違いに高い。
う日常生活レベルでは必要のないほど抽象的な線形空間とい世界では掛け算は行列積の形をしているんです。
そうやって解釈すれば、行列積を受け入れるのに抵抗が小さくなりますね。
世界観が違う。抽象度を上げた結果、掛け算の形が変わってしまった。
次元を増やしていくと物の動き方とか見え方が変わるように、掛け算の規則が変わってしまったと理解しました。
逆に言うと、高度な抽象化と一般化の能力を持つ天才には実生活レベルで僕ら凡人には見えない線形性、行列積の概念が見えているのかもしれない。
行列積を連立方程式としてとらえる
抽象的な線形性の概念は一次の連立方程式も線形変換にも応用できますね。
というか線形性の定義からこいつが行列積の発端に近い位置にいるんじゃないかとさえ思えます。
より原始的な概念というか、歴史的には一次の連立方程式を扱いやすくしたのが行列じゃないかなあ、と。
$\mathbb A = \begin{pmatrix}1 & 2 \\ -3 & -4\end{pmatrix}$という行列を作ります。
基底ベクトル$\begin{pmatrix}x\\y \end{pmatrix}$に作用させているとみることができます。
$\mathbb A = \begin{pmatrix}1 & 2 \\ -3 & -4\end{pmatrix}\begin{pmatrix}x\\y \end{pmatrix} = \begin{eqnarray} \left\{ \begin{array}{l} x + 2y \\ -3x + -4y \end{array} \right. \end{eqnarray}$
続く。
数学を学ぶモチベーション
僕の数学を学ぶモチベーションについて簡単にお話します。
数学を学び始めて感じるようになった、数学を学習する利点です。
出発点は力学などの専門書をストレスなく理解できるようになりたいと思ったことす。
掘り進めていくとバイオメカニクス、投資、戦略、心理学、コンピューターなどの学問は全てって数学へ行き着きます。
何を学んでも結局のところ数学が壁として立ちはだかってきます。
学問てなんだか話が難しくなって理解できなくなる瞬間てありますよね。大体が数学的な概念、論理が登場した時で、ほとんどの人はそこでモチベーションを失って諦めてしまうと思います。過去の僕がそうでした。
数学的な理解(根本的な論理)まではいかなくても、大体は理解できているからいいやって考えてましたね。
でもやっぱり、その程度の浅い理解のままだと本質は見えてこないんです。
本質が見えてこないと誰かの価値観に振り回されて消耗して人生は終わってしまいます。
僕の言っていることが間違っていた場合、僕を信頼してトレーニングしている選手達は人生を浪費することになります。
このブログの読者の皆様も人生の貴重な時間を費やしているはずなので、緩やかに僕と心中してしまっている可能性は否定できません(僕は否定しますが)。
膝理論だったり母指球理論だったり(僕は否定します)。
本当はもっと力を発揮できるポテンシャルがあったのにって人はボクシング界には沢山いたんじゃないかと思ってます。
本質的な知識、論理性を持ってることは生きる上で重要なことで、時に身を助けたりしてくれますよね。
投資詐欺なんかがその典型例だと思います。
金になります!インデックスなら安心です!この投資先は絶対に損しません!って国やメディアの喧伝を買ってしまうと財産を失ってしまうこともあり得ます。
今なんて流行り病のプロモーションが進行しているので、科学は正しい(メディアや国)って観念だけで下手な決断を下すと命すら盗られてしまう環境ですからね。
数学って本当に難しいんですが、数学の論理の組み立て方や数学が描く抽象的な世界観が慣れてくると、趣味であり実用でもあるコンピューターや投資の専門書を読むストレスが本当に小さくなります。これだけでも数学を勉強する価値があるなーって思います。
とても難しいんですけど、苦しむ過程で論理を組み立てていく癖がつきます。見る角度を変えて景色を一変させる経験や長い論理を紐解いていく作業に脳が慣れていって、癖にすらなります。
「ガードが下がる」の原因を「怠惰なだけ」に結び付けて結論するようなことがなくなるんです。
人の行動論理や思考パターンも抽象化してどんな論理でこの人は動いているんだろうって考えるようになりました。理解するのは難しいですが。
選手の言動から根底にある彼らの価値観を見出して動機づけできるようになってきていると感じます。
恐らく、それは長い論理、本質的な因果関係を構築しようとする脳神経へ変化しているからです。数学で獲得したニューロン結合が勝手反応して情報処理をやるんですよね、きっと。
「本当にチャンピオンになりたいのか?」「ボクシングが好きで長く続けたいだけじゃないか?」「言動が一致しない」って選手の言動の因果関係、論理を無意識に組み立ててしまいます。
論理性が高まるってことですね。数学は難しいですが、それを理解しようと苦しむ過程で手に入れた様々な観念が生活を充実させてくれます。
これだけでも学ぶ価値があると思います。


コメント